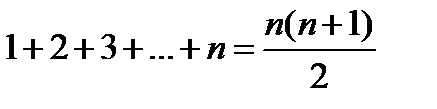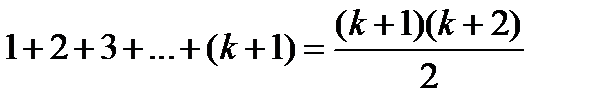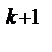несколько прямых делят плоскость на части докажите что эти части можно

Несколько прямых делят плоскость на части докажите что эти части можно

Несколько прямых делят плоскость на части. Докажите, что эти части можно раскрасить в 2 цвета так, что граничащие части будут иметь разный цвет.

Подсказка

Рассуждайте, используя индукцию по количеству прямых.

Решение

Будем использовать индукцию по количеству прямых n. При n = 1 утверждение задачи очевидно: достаточно покрасить две полуплоскости, на которые одна прямая делит плоскость, в разные цвета. Пусть утверждение задачи верно для k прямых. Рассмотрим некоторые k + 1 прямых. «Забывая» пока про (k+1)-ю прямую, раскрасим области, на которые делят плоскость остальные k прямых, в два цвета так, что граничащие части будут иметь разный цвет (это можно сделать по предположению индукции). При такой раскраске области, граничащие по (k+1)-й прямой, будут иметь одинаковый цвет. Далее перекрасим все области, расположенные по одну из сторон относительно (k+1)-й прямой, в противоположный цвет. Полученная в результате раскраска удовлетворяет условию задачи.

Источники и прецеденты использования

книга
Автор	Алфутова Н.Б., Устинов А.В.
Год издания	2002
Название	Алгебра и теория чисел
Издательство	МЦНМО
Издание	1
глава
Номер	1
Название	Метод математической индукции
Тема	Индукция
параграф
Номер	3
Название	Индукция в геометрии и комбинаторике
Тема	Индукция (прочее)
задача
Номер	01.054
web-сайт
задача

Источник

Доказательство тождеств.

Доказать, что при любом натуральном nсправедливо равенство

1) Проверим, что это тождество верно при n = 1.

— верно.

2) Пусть тождество верно и для n = k, т.е.

3)Докажем, что это тождество верно и для n = k + 1, т.е.

Что и требовалось доказать.

Пример 21.

Доказать формулу

1) . Левая часть равна 1. Правая часть . Следовательно, при верно.

2)

3) n= .

Действительно, = = , что и требовалось доказать.

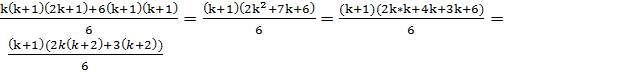
Пример22.

1) При n=1. 1 3 =1 2 – верно.

2) При n=k. 1 3 +2 3 +3 3 +4 3 +…+k 3 =(1+2+3+4+…+k) 2 – верно.

Пример 23.

1) Проверим, что это тождество верно при n = 2.

2) Пусть тождество верно для n = k, т.е.

3) Докажем, что это тождество верно и для n = k + 1, т.е.

2 2 + 3 2 + 4 2 + …+ k 2 + (k + 1) 2 = k 2

= (k –1 + k + 1) 2 = 2k 2 = k 2

Пример 24.

Докажите тождество …

При n 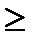2

1) Проверим, что это тождество верно для n = 2

— верно

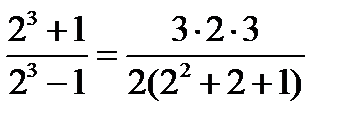
2) Пусть формула верна для n = k, т.е.

…

3) Докажем, что эта формула верна и для n = k + 1, т.е.

… = = = =

Докажите тождество

1.Проверим, что это тождество верно при n = 1.

2.Пусть тождество верно и для n = k, т.е.

1 3 −2 3 +3 3 −4 3 + …+(2k−1) 3 −(2k) 3 = −k 2 (4k+3)

3.Докажем, что это тождество верно и для n = k + 1, т.е.

1 3 −2 3 +3 3 −4 3 + …+(2k−1) 3 −(2k) 3 +(2(k+1) −1) 3 −(2(k+1)) 3 =

М – сумма 2) и 3).

М = = =

= =

= = =

= = =

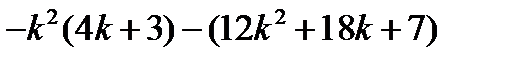
Задачи на геометрическую прогрессию.

Пример 26.

Докажем, что общий член геометрической прогрессии равен

1) Проверим, что данное утверждение верно при п=1 :

левая часть = правой части.

2) Предположим, что данное утверждение верно, при п=k:

3) И, докажем, что данное утверждение верно при п = k+1:

что и требовалось доказать.

Sn = (q≠1).

1) Проверим, что данное утверждение верно при п=1 :

Правая часть:

2) Предположим, что данное утверждение верно, при п=k:

S_k =

3)И, докажем, что данное утверждение верно при п=k+1:

S_k+1 = .

= .

Оба условия принципа математической индукции выполняются, поэтому формула Sn= верна для любого натурального п.

Логические задачи.

Пример 28.

На доске написаны два числа 1; 1. Вписав между числами их сумму, мы получим числа 1; 2; 1. Повторив эту операцию ещё раз, получим числа 1; 3; 2; 3; 1. После трёх операций будут числа 1; 4; 3; 5; 2; 5; 3; 4; 1. Какова будет сумма всех чисел на доске после 100 операций?

Решение. Ясно, что для выполнения 100 операций нам не хватит ни места, ни времени. Значит, нужно пытаться найти какую-то общую формулу для суммы чисел после n операций (обозначим её Sn ). Посмотрим на таблицу и найдем закономерность.

На самом деле можно не выписывать числа, а сразу сказать, как изменится сумма после добавления новых чисел. Пусть сумма была равна S. Разобьём каждое новое число в сумму двух старых. Например, от

1; 1 + 3; 3; 3 + 2; 2; 2 + 3; 3; 3 + 1; 1:

Каждое старое число (кроме двух крайних единиц) входит теперь в сумму три раза, поэтому новая сумма равна 3S − 2 (мы вычли 2, чтобы учесть недостающие единицы). Поэтому S5 = 3S4 − 2 = 244 и вообще Sn = 3Sn−1 − 2: Попробуем составить общую формулу. Если бы не вычитание двух единиц, то каждый раз сумма увеличивалась бы в три раза, как в степенях тройки (1; 3; 9; 27; 81; 243; : : : ). А наши числа, как теперь видно, на единицу больше. Таким образом, можно предположить, что Sn = 3n + 1. Докажем это по индукции.

1) N=1. Смотри таблицу (для n = 0; 1; 2; 3).

2) Если Sn−1 = 3n−1 + 1; то Sn = 3Sn−1 − 2 = 3(3n−1 + 1) − 2 = 3 · 3n−1 + 3 − 2 = 3n + 1, что и требовалось доказать. Из формулы видно, что после ста операций сумма всех чисел на доске будет равна 3100 + 1. Задача решена.

Пример 29.

Несколько прямых делят плоскость на части. Доказать, что можно раскрасить эти части в белый и чёрный цвет так, чтобы соседние части (имеющие общий отрезок границы) были разного цвета.

Заметим, что не любую картинку можно так раскрасить. Например, если в одной точке сходятся несколько прямых, то одна из них может быть белой, а две другие, хоть и граничат между собой, будут черными. Но для плоскости, разделенной на части прямыми,

это произойти не может. Докажем это.

Пусть прямая только одна. Тогда всё просто: одна полуплоскость белая, другая – чёрная.

Если прямых две, получатся четыре части. Посмотрим, что произойдёт, если мы на рисунке с двумя прямыми и четырьмя частями проведём третью прямую. Она поделит три части из четырёх; при этом появятся новые участки границы, по обе стороны

которых цвет один и тот же. Что же делать? С одной стороны от новой прямой поменяем цвета (белый на черный и наоборот) и получим раскраску, соответствующую условию. Тогда, используя этот метод, мы можем добавить еще сколько угодно прямых. Что и требовалось доказать.

Пример 30.

Наша задача доказать, что возможно переместить на другой стержень пирамидку из любого числа колец, соблюдая правила игры.

Пусть в пирамидке три кольца. Временно забудем про нижнее, самое большое (мысленно приклеим его к основанию). Тогда останется пирамидка из двух колец, которую мы уже умеем перекладывать. Переложим её с первого стержня на третий. После этого вспомним про большое кольцо и переложим его на второй стержень (который пока пуст). Теперь переложим пирамидку из двух верхних колец с третьего стержня на второй. Теперь, зная, как перекладывать пирамидку из трех колец, мы можем переложить четыре кольца (достаточно в наших предыдущих рассуждениях заменить пирамидку из двух колец на пирамидку из трёх). После этого можно переложить пять колец, зная, как перекладывать четыре кольца, и так далее. Что и требовалось доказать.

Геометрические задачи.

Пример 31.

Найти, на сколько частей делит прямую n точек.

Рассмотрим 1 точку. Она делит прямую на 2 части. 2 точки делят прямую на 3 части, 3 точки на 4 части. Тогда мы можем предположить, что n точек делят прямую на N(n)=n+1 частей. Докажем это утверждение.

1) При n=1. Верно, так как мы рассмотрели это в рассуждениях.

2) Если добавленная точка расположена между какими то двумя, она разделит соединяющий эти точки отрезок на два. Если она расположена на луче, она добавит один отрезок. То есть добавление точки увеличивает число частей на 1. Значит: N(n+1)=N(n)+1=(n+1)+1. Следовательно, наше утверждение доказано.

Пример 32.

Доказать, что сумма внутренних углов любого n-угольника равна π(n-2).

Так как минимальный n-угольник – это треугольник, то на нашу задачу накладывается условие: n≥3.

1) При n=3. π*1=π – верно.

2) При n=k. π(k-2) – верно.

3) При n=k+1. π(k-1). Разобьем (k+1)-угольник на треугольник и k-угольник, проведя диагональ. Тогда сумма углов треугольника и

4) k-угольника равна π(n-2) (из 1 и 2 шага). Следовательно, сумма внутренних углов любого n-угольника равна π(n-2), что и требовалось доказать.

Пример 33.

Вычислить сторону правильного — угольника, вписанного в круг радиуса R.

При n=2 правильный 2 n – угольник есть квадрат; его сторона . Далее, согласно формуле удвоения

находим, что сторона правильного восьмиугольника , сторона правильного шестнадцатиугольника , сторона правильного тридцатидвухугольника . Можно предположить поэтому, что сторона правильного вписанного 2 n – угольника при любом равна

. (1)

Допустим, что сторона правильного вписанного — угольника выражается формулой (1). В таком случае по формуле удвоения

,

откуда следует, что формула (1) справедлива при всех n.

Пример 34.

На сколько треугольников n-угольник (не обязательно выпуклый) может быть разбит своими непересекающимися диагоналями?

Для треугольника это число равно единице (в треугольнике нельзя провести ни одной диагонали); для четырехугольника это число равно, очевидно, двум.

Предположим, что мы уже знаем, что каждый k-угольник, где k

Источник

Волжский класс

Боковая колонка

Рубрики

Видео

Книжная полка

Малина для Админа

Боковая колонка

Опросы

Календарь

Ноябрь 2021

Пн	Вт	Ср	Чт	Пт	Сб	Вс
« Окт
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

5 класс. Математика. Никольский. Учебник. Ответы к стр. 80

Измерение величин

Прямая. Луч. Отрезок

Ответы к стр. 80

346. Проведите прямую AB и вне ее точку C. Через точку C проведите прямую параллельную прямой AB.

347. Сколько прямых можно провести через одну точку?

348. Даны три точки, не лежащие на одной прямой. Через каждые две точки проведена прямая. Сколько прямых проведено?

349. Даны четыре точки так, что никакие три из них не лежат на одной прямой. Через каждые две точки проведена прямая. Сколько прямых проведено?

350. На сколько частей прямая делит плоскость?

351. На сколько частей делят плоскость две прямые, если они:
а) пересекаются; б) параллельны?

а) на 4 части;
б) на 3 части.

352. На сколько частей можно разделить плоскость тремя прямыми?

Если прямые параллельны — на 4 части, если пересекаются в одной точке — на 6 частей, если пересекаются не в одной точке — на 7 частей.

353. Отметьте на листе бумаги точку, проведите несколько лучей с началом в этой точке. Сколько таких лучей можно провести?

354. Отметьте на прямой две точки A и B. Сколько получилось лучей с началом в этих точках?

355. Сколько получится лучей, если на прямой отметить:
а) 3 точки; б) 5 точек; в) 100 точек?

Из одной точки выходят два луча.
а) 3 • 2 = 6 лучей;
б) 5 • 2 = 10 лучей;
в) 100 • 2 = 200 лучей.

356. Две прямые пересекаются в одной точке. Сколько лучей с началом в этой точке они образуют?

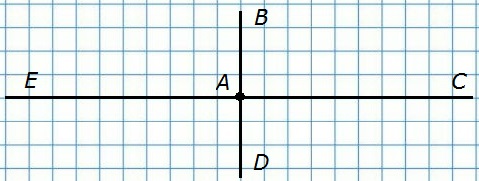
Лучи АС, АD, АЕ, АВ — всего 4 луча.

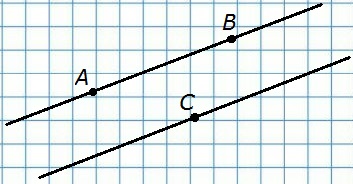
357. Назовите все лучи с вершиной в точках A, B и C (рис. 47). Сколько лучей получилось.

Лучи АM, АN, BM, ВN, CM, CN — всего 6 лучей.

358. Назовите все отрезки с концами в точках M, N и K (рис. 48). Сколько отрезков получилось?

Отрезки MА, MК, NК — всего 3 отрезка.

359. На прямой отметили четыре точки. Образовалось 6 отрезков с концами в этих точках. Проверьте.

Отрезки АВ, АС, АD, ВС, ВD, СD — всего 6 отрезков.

360. Перечертите рисунок 49 в тетрадь. Обозначьте все точки пересечения прямых, продолжив их, если нужно. На сколько частей разделилась плоскость? Выберите правильный ответ:
A. 10 частей;
Б. 11 частей;
В. 12 частей.

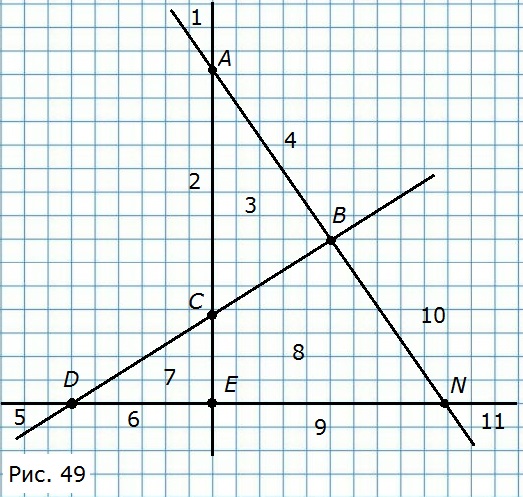
Ответ Б — 11 частей.

Источник