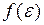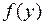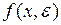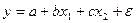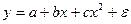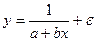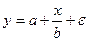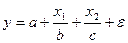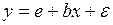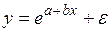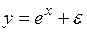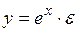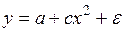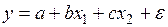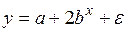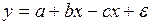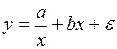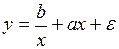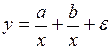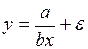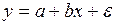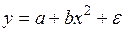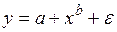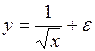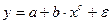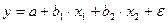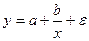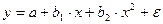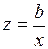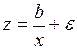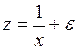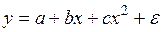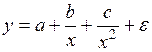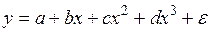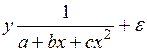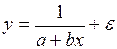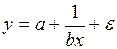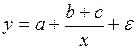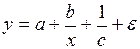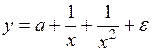оценить статистическую значимость нелинейного уравнения регрессии можно с помощью
Оценка параметров уравнения регреcсии. Пример
Задание:
По группе предприятий, выпускающих один и тот же вид продукции, рассматриваются функции издержек:
y = α + βx;
y = α x β ;
y = α β x ;
y = α + β / x;
где y – затраты на производство, тыс. д. е.
x – выпуск продукции, тыс. ед.
1. Уравнение имеет вид y = α + βx
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y- y ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 78 | 133 | 6084 | 17689 | 10374 | 142.16 | 115.98 | 83.83 | 1 |
| 82 | 148 | 6724 | 21904 | 12136 | 148.61 | 17.9 | 0.37 | 9 |
| 87 | 134 | 7569 | 17956 | 11658 | 156.68 | 95.44 | 514.26 | 64 |
| 79 | 154 | 6241 | 23716 | 12166 | 143.77 | 104.67 | 104.67 | 0 |
| 89 | 162 | 7921 | 26244 | 14418 | 159.9 | 332.36 | 4.39 | 100 |
| 106 | 195 | 11236 | 38025 | 20670 | 187.33 | 2624.59 | 58.76 | 729 |
| 67 | 139 | 4489 | 19321 | 9313 | 124.41 | 22.75 | 212.95 | 144 |
| 88 | 158 | 7744 | 24964 | 13904 | 158.29 | 202.51 | 0.08 | 81 |
| 73 | 152 | 5329 | 23104 | 11096 | 134.09 | 67.75 | 320.84 | 36 |
| 87 | 162 | 7569 | 26244 | 14094 | 156.68 | 332.36 | 28.33 | 64 |
| 76 | 159 | 5776 | 25281 | 12084 | 138.93 | 231.98 | 402.86 | 9 |
| 115 | 173 | 13225 | 29929 | 19895 | 201.86 | 854.44 | 832.66 | 1296 |
| 0 | 0 | 0 | 16.3 | 20669.59 | 265.73 | 6241 | ||
| 1027 | 1869 | 89907 | 294377 | 161808 | 1869 | 25672.31 | 2829.74 | 8774 |
2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции
Анализ точности определения оценок коэффициентов регрессии
S a = 0.1712
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-20.41;56.24)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается
Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим
Нелинейные модели регрессии



#Нелинейным является уравнение регрессии нелинейное относительно входящих в него …
#Если спецификация модели 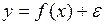
+
—
—
—
#Нелинейным не является уравнение …
+
—
—
—
#Нелинейным является уравнение …
+
—
—
—
#Нелинейное уравнение регрессии означает нелинейную форму зависимости между …
+результатом и факторами
-фактором и результатами
-результатом и параметрами
-фактором и случайной величиной
#Если спецификация модели отображает нелинейную форму зависимости между экономическими показателями, то нелинейно уравнение …
#Уравнение регрессии 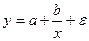
#Спецификация модели нелинейная парная регрессия подразумевает нелинейную зависимость и …
-пару независимых переменных
-пару зависимых переменных
-пару существенных переменных
#Нелинейным называется уравнение регрессии, если …
+независимые переменные входят в уравнение нелинейным образом
-параметры входят нелинейным образом, а переменные линейны
-зависимые переменные входят в уравнение нелинейным образом
-параметры и зависимые переменные входят в уравнение нелинейным образом
#В нелинейной модели парной регрессии 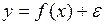
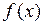
#Экспоненциальным не является уравнение регрессии …
+
—
—
—
#Примером нелинейной зависимости экономических показателей является …
+классическая гиперболическая зависимость спроса от цены
-линейная зависимость выручки от величины оборотных средств
-зависимость объема продаж от недели реализации
-линейная зависимость затрат на производство от объема выпуска продукции
#При выборе спецификации нелинейная регрессия используется, если …
+между экономическими показателями обнаруживается нелинейная зависимость
-между экономическими показателями не обнаруживается нелинейная зависимость
-нелинейная зависимость для исследуемых экономических показателей является несущественной
-между экономическими показателями обнаруживается линейная зависимость
#Было замечено, что при увеличении количества вносимых удобрений урожайность также возрастает, однако, по достижении определенного значения фактора моделируемый показатель начинает убывать. Для исследования данной зависимости можно использовать спецификацию уравнения регрессии …
+
—
—
—
#Известно, что с увеличением объема производства себестоимость единицы продукции уменьшается за счет того, что происходит перераспределение постоянных издержек. Пусть а – совокупная величина постоянных издержек, а b – величина переменных издержек в расчете на 1 изделие. Тогда зависимость себестоимости единицы продукции от объема производства можно описать с помощью модели …
+
—
—
—
#Если между экономическими показателями существует нелинейная связь, то …
+целесообразно использовать спецификацию нелинейного уравнения регрессии
-необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии
-нецелесообразно использовать спецификацию нелинейного уравнения регрессии
-целесообразно использовать линейное уравнение парной регрессии
#Парабола второй степени может быть использована для зависимостей экономических показателей, если
+если для определенного интервала значений фактора меняется характер связи рассматриваемых показателей: прямая связь изменяется на обратную или обратная на прямую
-если исходные данные не обнаруживают изменения направленности
-если для определенного интервала значений фактора меняется скорость изменений значений результата, то есть возрастает динамика роста или спада
-если характер связи зависит от случайных факторов
#Для моделирования зависимости предложения от цены не может быть использовано уравнение регрессии …
+
—
—
—
#Нелинейную модель зависимостей экономических показателей нельзя привести к линейному виду, если …
+нелинейная модель является внутренне нелинейной
-нелинейная модель является внутренне линейной
-линейная модель является внутренне нелинейной
-линейную модель является внутренне линейной
#Проводится исследование финансовых результатов деятельности предприятий, среди которых обнаруживаются как прибыльные, так и убыточные. Среди ряда факторов, влияющих на прибыль, был выделен доминирующий. При этом нельзя использовать спецификацию …
+
— 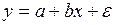
+выработки ль трудоемкости
-заработной платы от выработки
-выработки от уровня квалификации
-объема предложения от цены
#К линейному уравнению нельзя привести …
+
—
—
—
#Линеаризация подразумевает процедуру …
+приведения нелинейного уравнения к линейному виду
-приведения линейного уравнения к нелинейному виду
-приведения нелинейного уравнения относительно параметров к уравнению, линейному относительно результата
-приведения уравнения множественной регрессии к парной
#Уравнение 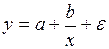
+
—
—
—
#Результатом линеаризации полиномиальных уравнений являются …
+линейные уравнения множественной регрессии
-нелинейные уравнения множественной регрессии
-линейные уравнения парной регрессии
-нелинейные уравнения парной регрессии
#Замена 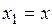
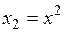
+
—
—
—
#Замена 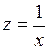
+
—
—
—
#Линеаризация не подразумеваетпроцедуру …
+включения в модель дополнительных существенных факторов
-приведения нелинейного уравнения к линейному
#Основной целью линеаризации уравнения регрессии является …
+возможность применения метода наименьших квадратов для оценки параметров
-улучшение качества модели
-повышение существенности связи между рассматриваемыми признаками
-получение новых нелинейных зависимостей
#Для нелинейных уравнений метод наименьших квадратов применяется к …
+преобразованным линеаризованным уравнениям
-не преобразованным линейным уравнениям
#Множественная регрессия не является результатом преобразования уравнения …
+
—
—
—
#К линейному виду нельзя привести …
+нелинейную модель внутренне линейную
-нелинейную модель внутренне нелинейную
-линейную модель внутренне нелинейную
-линейную модель внутренне линейную
#Величина коэффициента эластичности показывает …
+на сколько процентов изменится в среднем результат при изменении фактора на 1%
-во сколько раз измениться в среднем результат при изменении фактора в два раза
-предельно возможное значение результата
-предельно допустимое изменение варьируемого признака
#Спецификацию нелинейного уравнения парной регрессии целесообразно использовать, если значение…
+индекса детерминации, рассчитанного для данной модели достаточно близко к 1
-линейного коэффициента корреляции для исследуемой зависимости близко к 1
-индекса корреляции для исследуемой зависимости близко к 0
-доля остаточной дисперсии результативного признака в его общей дисперсии стремится к 1
#Если значение индекса корреляции для нелинейного уравнения регрессии стремится к 1, следовательно …
+нелинейная связь достаточно тесная
-линейная связь достаточно тесная
-нелинейная связь недостаточно тесная
-нелинейная связь отсутствует
#Оценить статистическую значимость нелинейного уравнения регрессии можно с помощью …
-средней ошибки аппроксимации
-линейного коэффициента корреляции
#Расчет средней ошибки аппроксимации для нелинейных уравнений регрессии связан с расчетом разности между …
+фактическим и теоретическим значениями результативной переменной
-фактическим и теоретическим значениями независимой переменной
-прогнозным и теоретическим значениями результативной переменной
-прогнозным и теоретическим значениями независимой переменной
#Назовите показатель корреляции для нелинейных моделей регрессии.
-линейный коэффициент корреляции
-парный коэффициент линейной корреляции
#Смысл расчета средней ошибки аппроксимации состоит в определении среднего арифметического значения …
+отклонений ε, выраженных в процентах от фактических значений результативного признака
-теоретических значений результативного признака, выраженных в процентах от его фактических значений
! отклонений ε, выраженных в процентах от фактических значений независимой переменной
-теоретических значений результативного признака, выраженных в процентах от его фактических значений признака
#Значение индекса детерминации, рассчитанное для нелинейного уравнения регрессии характеризует …
+долю дисперсии результативного признака, объясненную нелинейной регрессией в общей дисперсии результативного признака
-долю дисперсии результативного признака, объясненную линейной регрессией в общей дисперсии результативного признака
-долю дисперсии результативного признака, необъясненную нелинейной корреляцией в общей дисперсии результативного признака
-долю дисперсии результативного признака, объясненную линейной корреляцией в общей дисперсии результативного признака
#При хорошем качестве модели допустимым значением средней ошибки аппроксимации является …
#Значение индекса корреляции рассчитанное для нелинейного уравнения регрессии характеризует …
+тесноту нелинейной связи
-тесноту линейной связи
-тесноту обратной связи
-тесноту случайной связи
#Величина отклонений фактических значений результативного признака от его теоретических значений представляет собой …
Пример нахождения статистической значимости коэффициентов регрессии
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Анализ точности определения оценок коэффициентов регрессии
S a = 0.2704
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.
Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 94
(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (10;0.05) = 1.812
Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).