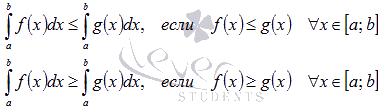постоянный множитель можно выносить за знак интеграла

Лекция 4. Определенный интеграл, его свойства и вычисление

Зміст

1. Понятие определенного интеграла

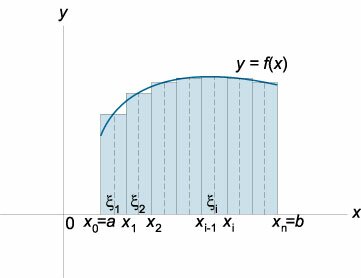
4) составим интегральную сумму функции y = f( x ) на отрезке [ a, b ]:

5) найдем предел интегральной суммы, когда λ → 0.

Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка [ a, b ] на частичные отрезки, ни от выбора точек z_i в них, то этот предел называется определенным интегралом от функции y = f( x ) на отрезке [ a, b ] и обозначается

В этом случае функция f( x ) называется интегрируемой на [ a, b ]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f( x ) – подынтегральной функцией, f( x ) dx – подынтегральным выражением, x – переменной интегрирования; отрезок [ a, b ] называется промежутком интегрирования.

Теорема 1. Если функция y = f( x ) непрерывна на отрезке [ a, b ], то она интегрируема на этом отрезке.

Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

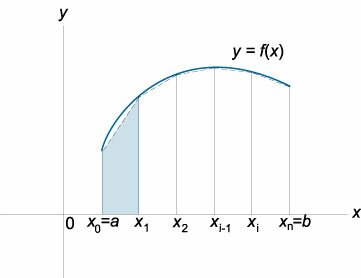
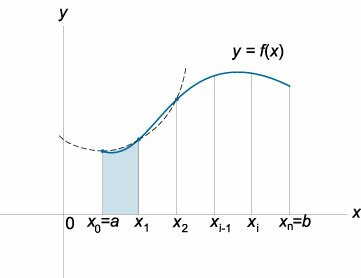
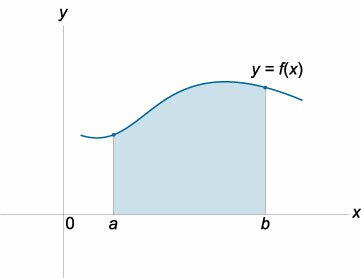
2. Геометрический смысл определенного интеграла

3. Основные свойства определенного интеграла

1. Значение определенного интеграла не зависит от обозначения переменной интегрирования:

2. Постоянный множитель можно выносить за знак определенного интеграла:

3. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:

4. Формула Ньютона–Лейбница

Теорема 2. Если функция y = f( x ) непрерывна на отрезке [ a, b ] и F(x) – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:

где символ называется знаком двойной подстановки.

Таким образом, формулу (2) можно записать в виде:

Пример 1. Вычислить интеграл

Решение. Для подынтегральной функции f( x ) = x 2 произвольная первообразная имеет вид

Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления интеграла возьмем первообразную, имеющую наиболее простой вид:

5. Замена переменной в определенном интеграле

Теорема 3. Пусть функция y = f( x ) непрерывна на отрезке [ a, b ]. Если:

1) функция x = φ ( t ) и ее производная φ ‘( t ) непрерывны при ;

2) множеством значений функции x = φ ( t ) при является отрезок [ a, b ];

которая называется формулой замены переменной в определенном интеграле.

В отличие от неопределенного интеграла, в данном случае нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования α и β (для этого надо решить относительно переменной t уравнения φ ( t ) = a и φ ( t ) = b ).

Пример 2. Вычислить интеграл

6. Интегрирование по частям

Теорема 4. Пусть функции u = u( x ) и v = v( x ) имеют непрерывные производные на отрезке [ a, b ]. Тогда имеет место следующая формула интегрирования по частям:

Пример 3. Вычислить

Источник

Постоянный множитель можно выносить за знак интеграла

Постоянный множитель можно выносить за знак определенного интеграла:
\(\large\int\limits_a^b\normalsize = k\large\int\limits_a^b\normalsize \)

Определенный интеграл от суммы функций равен сумме интегралов от этих функций:
\(\large\int\limits_a^b\normalsize <\left[ \right]dx> = \large\int\limits_a^b\normalsize + \large\int\limits_a^b\normalsize \)

Если верхний предел равен нижнему, то определенный интеграл равен нулю:
\(\large\int\limits_a^a\normalsize = 0\)

Пусть точка \(c\) принадлежит отрезку \(\left[ \right]\). Тогда определенный интеграл от функции \(f\left( x \right)\) на отрезке \(\left[ \right]\) равен сумме интегралов на частичных промежутках \(\left[ \right]\) и \(\left[ \right]\):
\(\large\int\limits_a^b\normalsize = \large\int\limits_a^c\normalsize + \large\int\limits_c^b\normalsize \)

Определенный интеграл от неотрицательной функции всегда больше или равен нулю:
\(\large\int\limits_a^b\normalsize \ge 0\;\;\text<если>\;\;f\left( x \right) \ge 0 \;\;\text<на>\;\left[ \right].\)

Определенный интеграл от неположительной функции всегда меньше или равен нулю:
\(\large\int\limits_a^b\normalsize \le 0\;\;\text<если>\;\;f\left( x \right) \le 0 \;\;\text<на>\;\left[ \right].\)

Источник

Свойства определенного интеграла.

В этой статье мы перечислим основные свойства определенного интеграла. Большинство этих свойств доказываются на основе понятий определенного интеграла Римана и Дарбу.

Вычисление определенного интеграла очень часто проводится с использованием первых пяти свойств, так что мы будем при надобности на них ссылаться. Остальные свойства определенного интеграла, в основном, применяются для оценки различных выражений.

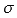
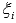
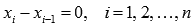
То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Это свойство является следствием определения интеграла Римана, так как в этом случае каждая интегральная сумма для любого разбиения промежутка [a; a] и любого выбора точек равна нулю, так как , следовательно, пределом интегральных сумм является ноль.

Для интегрируемой на отрезке [a; b] функции выполняется .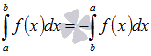

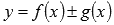
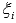
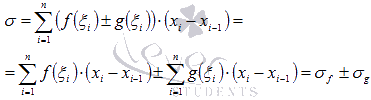
Запишем интегральную сумму функции для данного разбиения отрезка и данного выбора точек :

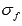
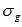
где и — интегральные суммы функций y = f(x) и y = g(x) для данного разбиения отрезка соответственно.

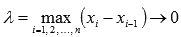
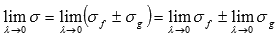
Переходя к пределу при получим , что по определению интеграла Римана равносильно утверждению доказываемого свойства.

Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке [a; b] функции y = f(x) и произвольного числа k справедливо равенство .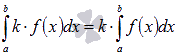

Доказательство этого свойства определенного интеграла абсолютно схоже с предыдущим:

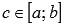
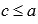
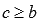
Это свойство справедливо как для , так и для или .

Доказательство можно провести, опираясь на предыдущие свойства определенного интеграла.

Доказательство основано на свойстве сумм Дарбу: если к имеющемуся разбиению отрезка добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя – не увеличиться.

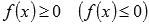
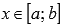
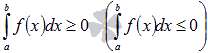
Если функция y = f(x) интегрируема на отрезке [a; b] и для любого значения аргумента , то .

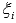
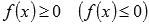
Это свойство доказывается через определение интеграла Римана: любая интегральная сумма для любого выбора точек разбиения отрезка и точек при будет неотрицательной (не положительной).

Для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x) справедливы неравенства:

Это утверждение означает, что допустимо интегрирование неравенств. Этим следствием мы будем пользоваться при доказательстве следующих свойств.

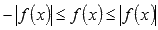
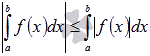
Очевидно, что . В предыдущем свойстве мы выяснили, что неравенство можно почленно интегрировать, поэтому, справедливо . Это двойное неравенство можно записать как .

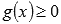
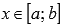
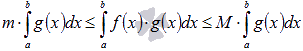
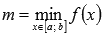
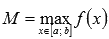
Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке [a; b] и для любого значения аргумента , тогда , где и .

Первая формула среднего значения.

Первая формула среднего значения в обобщенной форме.

Вторая формула среднего значения.

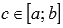
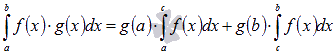
Если на отрезке [a; b] функция y = f(x) интегрируема, а y = g(x) монотонна, то существует такое число , что справедливо равенство .

Источник

Определённый интеграл и методы его вычисления

В каждой главе будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Понятие определённого интеграла и формула Ньютона-Лейбница

Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.

Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,

(38)

Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:

Поэтому формулу Ньютона-Лейбница будем записывать и так:

(39)

Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому

Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.

При a = b по определению принимается

Для того чтобы потренироваться в нахождении определённых интегралов, потребуется таблица основных неопределённых интегралов и пособие «Действия со степенями и корнями«.

Пример 1. Вычислить определённый интеграл

Решение. Сначала найдём неопределённый интеграл:

Применяя формулу Ньютона-Лейбница к первообразной

Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).

Пример 2. Вычислить определённый интеграл

Решение. Используя формулу

Найти определённый интеграл самостоятельно, а затем посмотреть решение

Пример 3. Найти определённый интеграл

.

Пример 4. Найти определённый интеграл

.

Свойства определённого интеграла

Теорема 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.

Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:

Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.

(40)

Пусть F(x) – первообразная для f(x). Для f(t) первообразной служит та же функция F(t), в которой лишь иначе обозначена независимая переменная. Следовательно,

На основании формулы (39) последнее равенство означает равенство интегралов

Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.

(41)

Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.

(42)

Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если

(43)

Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.

(44)

Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его, т.е.

(45)

Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если

Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство

можно почленно интегрировать, т.е.

(46)

Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.

Пример 5. Вычислить определённый интеграл

Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим

Определённый интеграл с переменным верхним пределом

Пусть f(x) – непрерывная на отрезке [a, b] функция, а F(x) – её первообразная. Рассмотрим определённый интеграл

(47)

,

а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х, которую обозначим через Ф(х), т.е.

(48)

Докажем, что функция Ф(х) является первообразной для f(x) = f(t). Действительно, дифференцируя Ф(х), получим

Функция Ф(х) – одна из бесконечного множества первообразных для f(x), а именно та, которая при x = aобращается в нуль. Это утверждение получается, если в равенстве (48) положить x = aи воспользоваться теоремой 1 предыдущего параграфа.

Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной

При выводе формулы интегрирования по частям было получено равенство u dv = d (uv) – v du. Проинтегрировав его в пределах от a до b и учитывая теорему 4 параграфа этой статьи о свойствах определённого интеграла, получим

Как это следует из теоремы 2 параграфа о свойствах неопределённого интеграла, первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде

получаем формулу интегрирования по частям для вычисления определенного интеграла:

(49)

Пример 6. Вычислить определённый интеграл

Найти определённый интеграл по частям самостоятельно, а затем посмотреть решение

Пример 7. Найти определённый интеграл

.

Пример 8. Найти определённый интеграл

.

Перейдём к вычислению определённого интеграла методом замены переменной. Пусть

где, по определению, F(x) – первообразная для f(x). Если в подынтегральном выражении произвести замену переменной

то в соответствии с формулой (16) можно записать

первообразная функция для

принимает соответственно значения aи b, т.е.

Но, согласно формуле Ньютона-Лейбница, разность F(b) – F(a) есть

(50)

Это и есть формула перехода к новой переменной под знаком определённого интеграла. С её помощью определённый интеграл

после замены переменной

преобразуется в определённый интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются новыми пределами и . Чтобы найти новые пределы, нужно в уравнение

поставить значения x = aи x = b, т.е. решить уравнения

относительно и . После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.

При вычислении определённого интеграла методом замены переменной часто бывает удобно выражать не старую переменную как функцию новой, а, наоборот, новую – как функцию старой.

Пример 9. Вычислить определённый интеграл

Решение. Произведём замену переменной, полагая

Найдём новые пределы интегрирования. Подстановка значений x = 4 и x = 5 в уравнение

Используя теперь формулу (50), получим

После замены переменной мы не возвращались к старой переменной, а применили формулу Ньютона-Лейбница к полученной первообразной.

Найти определённый интеграл заменой переменной самостоятельно, а затем посмотреть решение

Пример 10. Найти определённый интеграл

.

Пример 11. Найти определённый интеграл

.

Источник