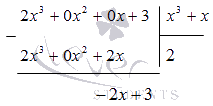правильную рациональную дробь можно представить в виде суммы простейших дробей следующим образом

Разложение правильной рациональной дроби в виде суммы простейших дробей с помощью метода неопределенных коэффициентов.

Разложение правильной рациональной дроби в виде суммы простейших дробей с помощью метода неопределенных коэффициентов.

Простыми дробями называются рациональные дроби вида или , где , а квадратный трехчлен не имеет действительных корней, т.е. дискриминант квадратного уравнения меньше нуля .

Правильной рациональной дробью называется дробь вида , где числитель и знаменатель представлен в виде многочлена, а степень числителя ниже степени знаменателя .

В случае если степень числителя выше степени знаменателя , то дробь называют неправильной. Если дробь является неправильной, то необходимо разделить числитель на знаменатель (по правилу деления многочленов), и представить дробь в виде суммы многочлена и правильной рациональной дроби :

Любая правильная рациональная дробь может быть представлена в виде суммы конечного числа простых рациональных дробей следующим образом:

Коэффициенты такого преобразованного выражения определяются методом неопределенных коэффициентов. Метод неопределённых коэффициентов ― это метод, используемый в математике для разложения искомой функции в виде линейной комбинации конечного или бесконечного набора базовых функций.

Рассмотрим прием разложения правильной рациональной дроби в виде суммы простейших дробей с неопределенными коэффициентами.

Алгоритм метода неопределенных коэффициентов

Чтобы разложить правильную рациональную дробь на простые дроби, необходимо выполнить следующие действия.

1. Разложить знаменатель на линейные и квадратные множители, которые не имеют действительных корней.

2. Записать разложение дроби в аналитической форме в виде простейших дробей с неопределенными коэффициентами.

В случае если в знаменателе присутствует сомножитель вида , то дробь раскладывается в следующем виде:

В случае если в знаменателе присутствует сомножитель вида , то дробь раскладывается в следующем виде:

3. Преобразуем полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях х.

4. Составляем систему уравнений из условия равенства коэффициентов при соответствующих степенях знаменателя в связи с тем, что аналитическая дробь с неизвестными коэффициентами равна исходной дроби. В результате получим систему линейных алгебраических уравнений относительно неизвестных коэффициентов разложения данной рациональной функции на сумму простейших. Решаем полученную систему уравнений для определения значений неопределённых коэффициентов. Следует отметить, что система уравнений для определения неизвестных коэффициентов разложения всегда имеет единственное решение.

Таким образом, выполняется разложение правильной рациональной дроби на сумму простых дробей. Рассмотрим задачи, которые решаются методом неопределённых коэффициентов.

Задача. Разложение дроби на простейшие

Необходимо представить правильную дробь в виде суммы простейших дробей. Для простоты задачи знаменатель рассматриваемой дроби представлен в виде произведения множителей.

1.Запишем разложение дробив аналитической форме в виде простейших дробей с неопределенными коэффициентами.

2. Преобразуем полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю.

3. Составляем систему уравнений из условия равенства коэффициентов при соответствующих степенях знаменателя.

Решая данную систему, получим, что неопределённые коэффициенты определяются следующим образом:

; ; ;

Таким образом, исходная рациональная дробь раскладывается на сумму простых дробей следующим образом:

Данный метод может использоваться как при аналитических выкладках, так и при компьютерном программировании для автоматизации процесса.

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

Источник

Разложение дроби на простейшие

Для закрепления материала будут рассмотрены несколько примеров и рассмотрена теория по разложению дробей на простейшие. Подробно рассмотрим метод неопределенных коэффициентов и метод частных значений, изучим всевозможные комбинации.

Простые дроби имеют название элементарных дробей.

Типы дробей

При упрощении выражения быстрее выполняются вычислительные функции. Представление дробно-рациональной дроби как суммы простейших дробей аналогично. Для этого применяют ряды Лорана для того, чтобы разложить в степенные ряды или для поиска интегралов.

Когда степень числителя многочлена меньше степени многочлена в знаменателе, имеет место разложение на простейшие дроби. Иначе применяется деление для выделения целой части, после чего производят разложение дробно-рациональной функции.

Применим деление углом. Получаем, что

Отсюда следует, что дробь примет вид

Алгоритм метода неопределенных коэффициентов

Для того, чтобы правильно произвести разложение, необходимо придерживаться нескольких пунктов:

Рассмотрим на нескольких примерах:

P 4 x + Q 4 ( x 2 + p x + q ) 4 + P 3 x + Q 3 ( x 2 + p x + q ) 3 + P 2 x + Q 2 ( x 2 + p x + q ) 2 + P 1 x + Q 1 x 2 + p x + q + + R 2 x + S 2 ( x 2 + r x + s ) 2 + R 1 x + S 1 x 2 + r x + s

Приведение полученной суммы простейших дробей при наличии неопределенного коэффициента к общему знаменателю, применяем метода группировки при одинаковых степенях х и получаем, что

Необходимо постоянно выполнять проверки. Это способствует тому, что приведение к общему знаменателю получит вид

Методом неопределенных коэффициентов считают метод разложения дроби на другие простейшие.

Использование метода частных значений способствует представлению линейных множителей таким образом:

По условию имеем, что степень многочлена числителя меньше степени многочлена знаменателя, тогда деление выполнять не нужно. Необходимо перейти к разложению на множители. для начала необходимо выполнить вынесение х за скобки. Получим, что

x 1 + x 2 = 5 x 1 · x 2 = 6 ⇔ x 1 = 3 x 2 = 2

Имея такой знаменатель, дробь раскладываем на простейшие дроби с неопределенными коэффициентами. Выражение примет вид:

Полученный результат необходимо приводить к общему знаменателю. Тогда получаем:

После упрощения придем к неравенству вида

Метод коэффициентов и метод частных значений отличаются только способом нахождения неизвестных. Данные методы могут быть совмещены для быстрого упрощения выражения.

По условию имеем, что степень числителя многочлена меньше знаменателя, значит зазложение примет вид

Производим приведение к общему знаменателю. Имеем, что

Приравняем числители и получим, что

157 = 8 C 3 ⇒ C 3 = 157 8

Поэтому подставим полученный значения в числитель, тогда

Раскроем скобки для того, чтобы привести подобные слагаемые с одинаковыми степенями. Придем к выражению вида

Итог решения – это искомое разложение дроби на простейшие вида:

При непосредственном применении метода неопределенных коэффициентов необходимо было бы решать все пять линейных уравнений, объединенных в систему. Такой метод упрощает поиск значения переменных и дальнейшее решение в совокупности. Иногда применяется несколько методов. Это необходимо для быстрого упрощения всего выражения и поиска результата.

Источник

Метод неопределённых коэффициентов для разложения дроби на сумму простейших дробей

Простейшие дроби

$x^2+7x+30$ – не раскладывается.

Обобщая, получаем следующее определение:

Простейшими (элементарными) дробями называют дроби вида:

Примеры простейших дробей:

Любая рациональная алгебраическая дробь может быть разложена на сумму простейших дробей, и притом единственным способом.

Алгоритм разложения дроби на сумму простейших дробей

Попробуем её разложить на две простейшие дроби следующим образом:

Дроби равны, знаменатели равны, значит, должны быть равны и числители:

4 x+ 1 = A(x-3)+B(x+10) = (A+B) x+ (-3A+10B)

Теперь используем важнейшее свойство многочленов:

У равных многочленов коэффициенты при соответствующих степенях переменной равны.

Получаем представление дроби в виде суммы простейших дробей:

Этот способ разложения был предложен в 17 веке Декартом и получил название «метода неопределённых коэффициентов».

Алгоритм метода неопределённых коэффициентов

Примеры

Пример 1. Разложите на простейшие дроби:

Раскладываем знаменатель на множители:$ x^2+5x+6 = (x+2)(x+3)$

Записываем разложение с неопределенными коэффициентами:

Приравниваем коэффициенты при одинаковых степенях x:

Записываем разложение с неопределенными коэффициентами:

Записываем разложение с неопределенными коэффициентами:

Раскладываем знаменатель на множители:$ 9x^2-4 = (3x-2)(3x+2)$

Записываем разложение с неопределенными коэффициентами:

Пример 2*. Разложите на простейшие дроби:

Источник

Разложение правильной рациональной дроби на сумму простейших дробей

Разложение правильной рациональной дроби на сумму простейших дробей

положительной рациональной дробью является Q (x), знаменатель кратности Q (x) по корням a имеет вещественный коэффициент с вещественным числом a, т. е.. Q (x)=(x-a) AF(x), где f(a)=^=0. (8.35) к этой дроби применяется следующее выражение: R (h)_ _ _ A___, f (h)_ _ /o ZB М(х) (х-а) (х-а)

Д О К а з а т е л ь с Т В О. он представляет собой по.- Действительное число A=—, учитывая разницу F (a) Если * F (a)#=0, то число A всегда Людмила Фирмаль

определяется(8.35).§3. Класс 313 интегрируемых функций в базовой функции P (x)_ _ _ _ и Q (x) (x-a)»‘ Если мы примем эту разницу к общему знаменателю、 R (x)_ _ _ _ A_R(x) — 4F (x) f (x)Q (x)»(x-a) a f(x)) Где f(x) представляет собой многочлен с коэффициентами вида f(x)=P(x)—DF (x). Так как F(a)=P(a)—Aq>(a) — P(d), то целое число a является корнем некоторого многочлена f (z;).Кратность y>1. Это означает, что f (a) t^0 (8.38)по вещественным коэффициентам является представлением, которое верно- (х-а) Ф(Х) * реальный» 1, f (x) — многочлен с вещественным коэффициентом, таким что последняя дробь (8.41) справа является правильной.314 ГЛ. 8. Первичные и

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Методы разложения рациональных дробей на простейшие

Далее мы приводим наиболее эффективные методы разложения правильной рациональной дроби на простейшие.

Общий вид разложения рациональной дроби на простейшие

Например,
.
Здесь A, B, C, D, E – неопределенные коэффициенты (действительные числа), которые нужно определить.

Методы разложения рациональной дроби на простейшие

На практике, удобно комбинировать эти методы. Разберем их применение на конкретных примерах.

Пример

Разложить правильную рациональную дробь на простейшие.

Сделаем проверку. Для этого определим C первым способом. Подставим в (1.2) x = 0 :
0 = 6 A – 6 B + 6 C + 3 D + 2 E ;
;
. Все правильно.

Определение коэффициента при старшей степени 1/(x–a)

Поэтому в предыдущем примере мы сразу могли искать разложение в виде:

.

В некоторых простых случаях, можно сразу определить коэффициенты разложения. Например,

.

Пример с комплексными корнями знаменателя

Теперь разберем пример, в котором знаменатель имеет комплексные корни.

Пусть требуется разложить дробь на простейшие:
.

1. Устанавливаем общий вид разложения:
.
Здесь A, B, C, D, E – неопределенные коэффициенты (действительные числа), которые нужно определить.

Источник