сколько диагональных сечений можно провести через одно боковое ребро в четырехугольной призме

Сколько диагональных сечений можно провести через одно боковое ребро в четырехугольной призме

§ 7. Параллелепипеды и призмы.

1. Определить диагонали прямоугольного параллелепипеда по трём его измерениям: 1) 1; 2; 2; 2) 2; 3; 6; 3) 6; 6; 7; 4) 8; 9; 12; 5) 12; 16; 21.

2. 1) Боковое ребро прямого параллелепипеда равно 5 м, стороны основания равны 6 м и 8 м и одна из диагоналей основания равна 12 м. Определить диагонали параллелепипеда.

2) В предыдущей задаче заменить данные числа по порядку следующими: 9 см, 7 см, 11 см и 14 см.

3. В прямом параллелепипеде стороны основания 3 см и 5 см, а одна из диагоналей основания 4 см. Меньшая диагональ параллелепипеда с плоскостью основания составляет угол в 60°. Определить диагонали параллелепипеда.

4. В прямом параллелепипеде стороны основания равны 2 см и 5 см; расстояние между меньшими из них 4 см; боковое ребро равно 2√ 2 см. Определить диагонали параллелепипеда.

5. Определить диагонали прямого параллелепипеда, у которого каждое ребро равно а, а угол основания равен 60°.

6. 1) В прямом параллелепипеде стороны основания длиной 3 см и 4 см составляют угол в 60°, а боковое ребро есть средняя пропорциональная между сторонами основания. Определить диагонали этого параллелепипеда.

2) В прямом параллелепипеде рёбра, выходящие из одной вершины, равны 1 м, 2 м и 3 м, причём два меньших образуют угол в 60°. Определить диагонали этого параллелепипеда.

7. Ребро куба равно а. Определить расстояние от вершины куба до его диагонали.

8. Ребро куба равно а. Найти кратчайшее расстояние от диагонали до непересекающего её ребра.

9. Доказать, что во всяком параллелепипеде сумма квадратов диагоналей равна сумме квадратов всех рёбер.

10. 1) В прямоугольном параллелепипеде стороны основания равны 7 дм и 24 дм, а высота параллелепипеда равна 8 дм. Определить площадь диагонального сечения.

11. В прямом параллелепипеде боковое ребро равно 1 м, стороны основания равны 23 дм и 11 дм, а диагонали основания относятся как 2:3. Определить площади диагональных сечений.

12. В прямом параллелепипеде стороны основания 17 см и 28 см; одна из диагоналей основания равна 25 см; сумма площадей диагональных сечений относится к площади основания, как 16:15. Определить площади диагональных сечений.

13. В прямом параллелепипеде с основанием ABCD дано: АВ=29 см, AD = 36 см, BD = 25 см и боковое ребро равно 48 см. Определить площадь сечения AB₁С₁D.

14. В прямом параллелепипеде острый угол основания содержит α°; одна из сторон основания равна а; сечение, проведённое через эту сторону и противоположное ей ребро, имеет площадь Q и образует с плоскостью основания угол 90° — α°. Определить другую сторону основания.

15. Основанием наклонного параллелепипеда служит ромб ABCD, в котором / BAD = 60°; боковые рёбра наклонены к плоскости основания под углом в 60°, и плоскость АА₁С₁С перпендикулярна к плоскости основания. Доказать, что площади сечений BB₁D₁D и АА₁С₁С относятся как 2 : 3.

16. (Устно.) Сколько диагоналей можно провести в четырёхугольной призме? в пятиугольной? в треугольной? в n-угольной?

17. (Устно.) Сколько плоских углов в пятиугольной призме? сколько двугранных? сколько трёхгранных?

18. (Устно.) 1) Какие фигуры представляют собой диагональные сечения параллелепипеда? 2) Сколько диагональных сечений можно провести в пятиугольной призме через одно её ребро? 3) На сколько частей эти плоскости (вопрос 2) делят данную призму? 4) Какое тело представляет каждая из этих частей (вопросы 2 и 3)?

19. (Устно.) Сколько диагональных сечений можно провести в n-угольной призме через все её боковые рёбра?

2) Определить диагональ правильной четырёхугольной призмы, если диагональ основания равна 8 см, а диагональ боковой грани равна 7 см.

21. Если в правильной четырёхугольной призме ABCDA₁B₁C₁D₁ диагонали B₁D и D₁B взаимно перпендикулярны, то диагонали А₁С и B₁D образуют угол в 60°. Доказать.

22. В правильной четырёхугольной призме площадь боковой грани равна Q. Определить площадь диагонального сечения.

23. Основанием призмы служит правильный шестиугольник со стороной а; боковые грани — квадраты. Определить диагонали этой призмы и площади её диагональных сечений.

24. Внутри правильной шестиугольной призмы, у которой боковые грани —квадраты, провести плоскость через сторону нижнего основания и противолежащую ей сторону верхнего основания. Сторона основания равна а. Определить площадь сечения.

25. Каждое ребро правильной треугольной призмы а = 3м. Через сторону основания и середину оси проведена плоскость. Найти площадь сечения.

26. Сторона основания правильной четырёхугольной призмы равна 15; высота равна 20. Найти кратчайшее расстояние от стороны основания до непересекающей её диагонали призмы.

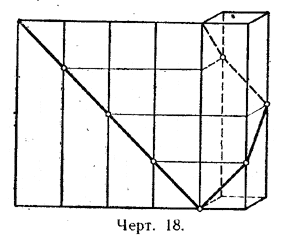
27. Квадрат с проведённой в нём диагональю свёрнут в виде боковой поверхности правильной четырёхугольной призмы, и, таким образом, диагональ квадрата обратилась в ломаную линию (не плоскую). Определить угол между смежными её отрезками (черт. 18).

28. В прямой треугольной призме через одну из сторон основания проведена плоскость, пересекающая противоположное боковое ребро и отклонённая от плоскости основания на 45°. Площадь основания равна Q. Определить площадь сечения.

29. В прямой треугольной призме стороны основания равны 10 см, 17 см и 21 см, а высота призмы 18 см. Определить площадь сечения, проведённого через боковое ребро и меньшую высоту основания.

30. Основанием прямой призмы служит ромб; диагонали призмы равны 8 см и 5 см; высота 2 см. Найти сторону основания.

31. Боковое ребро l =15 см наклонной призмы наклонено к плоскости основания под углом α = 30°. Определить высоту призмы.

32. В треугольной призме (наклонной) из двугранных углов между боковыми гранямидва содержат: 20°43’28» и 105°27’32». Чему равен третий угол?

33. В треугольной призме (наклонной) расстояния между боковыми рёбрами 37 см, 13 см и 40 см. Найти расстояние между большей боковой гранью и противолежащим боковым ребром.

Источник

Ответы в виде таблицы.
Сколько диагоналей имеют треугольная, четырёхугольная,
шестиугольная и n-угольная
призмы?

Сколько диагональных сечений можно провести через одно
боковое ребро в треугольной, четырёхугольной, шестиугольной и n-угольной призме?

В правильной шестиугольной призме сторона основания равна m, а боковые грани –
квадраты. Найдите диагонали призмы и площади диагоналей сечений.

Сколько диагоналей имеют треугольная, четырёхугольная,
шестиугольная и n-угольная
призмы?

Сколько диагональных сечений можно провести через одно
боковое ребро в треугольной, четырёхугольной, шестиугольной и n-угольной призме?

В правильной шестиугольной призме сторона основания равна m, а боковые грани –
квадраты. Найдите диагонали призмы и площади диагоналей сечений.

Смотри фотку по ходу это не уравнение а упростить выражение получилось так

На уровне знаний 9 класса дается построение графика квадратичной функции с помощью выделения квадрата из квадратного трехчлена.

Теперь исследуем полученную функцию чтобы построить ее график

В нашем примере а=1 > 0, значит ветви параболы направлены вверх.

Вычислим координаты нескольких точек параболы

При х = 0 у = 2, при х = 0 у = 0, при х = 1 у = 0, при х = 3 у = 2

и построим график. Смотри на фото.

Источник

Ответы в виде таблицы.
Сколько диагоналей имеют треугольная, четырёхугольная,
шестиугольная и n-угольная
призмы?

Сколько диагональных сечений можно провести через одно
боковое ребро в треугольной, четырёхугольной, шестиугольной и n-угольной призме?

В правильной шестиугольной призме сторона основания равна m, а боковые грани –
квадраты. Найдите диагонали призмы и площади диагоналей сечений.

Сколько диагоналей имеют треугольная, четырёхугольная,
шестиугольная и n-угольная
призмы?

Сколько диагональных сечений можно провести через одно
боковое ребро в треугольной, четырёхугольной, шестиугольной и n-угольной призме?

В правильной шестиугольной призме сторона основания равна m, а боковые грани –
квадраты. Найдите диагонали призмы и площади диагоналей сечений.

Для нахождения точек пересечения функции с осью необходимо положить

D>0, значит квадратное уравнение имеет два действительных корня.

Точки пересечения функции с осью имеют координаты

Для нахождения точек пересечения функции с осью необходимо положить

Итак, точки пересечения функции с осью имеет координаты

Источник

Справочный материал и задачи по теме «Призма»

Выбранный для просмотра документ Призма. Справочный материал и задачи.docx

Призма. Виды призмы

Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.

Мы же поведем подробный разговор.

Боковые грани – все грани, кроме оснований ( являются параллелограммами ).

Боковые ребра – общие стороны боковых граней ( параллельны между собой и равны ).

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.

Диагональное сечение –пересечение призмы и диагональной плоскости.

Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

Среди прямых призм выделяют правильные.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).

Параллелепипед – это призма, основаниями которой являются параллелограммы.

Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).

Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Частный случай прямоугольного параллелепипеда – куб.

Куб – прямоугольный параллелепипед, все грани которого – квадраты.

Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике

Вопросы для повторения:

— Что называется многогранником?

— Из каких частей состоит многогранник?

— Что называется гранью многогранника?

— Что называют диагональю многогранника?

Общие теоретические сведения

Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и n параллелограммов .

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы

Основания призмы являются равными многоугольниками.

Боковые грани призмы являются параллелограммами.

Боковые ребра призмы параллельны и равны.

Различают призмы прямые,наклонныеи правильные. (слайд 6,7,8)

Диагональным сечением призмы называется ее сечение плоскостью, проходящей через два боковых ребра, которые не лежат в одной грани.

Если секущая плоскость пересекает все боковые ребра призмы и перпендикулярна им, то получающееся при этом сечение называется перпендикулярным сечением призмы.

Площадь боковой поверхности призмы равна сумме площадей ее боковых граней.

Площадь полной поверхности призмы равна сумме площадей оснований и площади боковой поверхности.

.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

.

Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.

.

, где S – площадь основания, H – высота призмы.

Объем призмы можно найти, умножив площадь перпендикулярного сечения на длину бокового ребра. .

Частным случаем призмы является параллелепипед.

Параллелепипед– это призма, основаниями которой являются параллелограммы

Различают прямой, наклонный, прямоугольный параллелепипеды.

Длины непараллельных ребер прямоугольного параллелепипеда называют его линейными размерами (измерениями).

У прямоугольного параллелепипеда три измерения.

Объём прямоугольного параллелепипеда равен произведению трех его измерений.

Повтори необходимые формулы :

1. Прямоугольный параллелепипед

Пусть a, b, с – стороны, d – диагональ параллелепипеда,

S_n – полная поверхность.

d 2 = a 2 + b 2 + c 2

d=a

Ответь на теоретические вопросы по теме «Призма»

Ребро куба равно a. Найдите: диагональ грани, диагональ куба, периметр основания, площадь грани, площадь диагонального сечения; площадь поверхности куба; периметр и площадь сечения, проходящего через концы трёх рёбер, выходящих из одной и той же вершины. (слайд 14)

Существует ли призма, имеющая 50 рёбер? 54 ребра?

Решение: Число ребер n – угольной призмы 3n, поэтому призмы, имеющей 50 ребер, не существует, а 54 ребра имеет 18-угольная призма.

В правильной треугольной призме плоскость сечения BCА₁ образует с плоскостью основания двугранный угол φ. Постройте линейный угол этого двугранного угла. Дайте объяснение.

Построение: Проведём из вершины A правильного треугольника ABC высоту AK. Точка K принадлежит ребру BC. Соответственно, отрезок А₁К перпендикулярен ребру BC (по теореме о трёх перпендикулярах). Угол A₁КА– искомый.

1. Объем прямоугольного параллелепипеда равен 2. Чему будет равен объем параллелепипеда, если каждое его ребро увеличить в 3 раза.

Решение. Пусть ребра данного параллелепипеда равны a, b и c. Тогда имеем: V=abc=2. После увеличения каждого ребра в 3 раза его объём будет равен

V=3a*3b*3c =27 abc=27*2=54.

2. Аквариум имеет форму прямоугольного параллелепипеда высотой 30 см. Если в него налить 30 л. воды, то до верхнего края останется 5 см. Сколько литров воды нужно, чтобы наполнить пустой аквариум доверху?

Решение. Пусть V и H соответственно объем и высота параллелепипеда.

После заполнения пустого аквариума доверху H=30. Значит, 30*S=V.

Найдем отношение =, V=36 л.

3. Кубик весит 10 гр. Сколько граммов будет весить кубик, ребро которого в 3 раза больше, чем ребро первого кубика, если оба кубика изготовлены из одинакового материала.

Решение. Пусть V- объём данного параллелепипеда. После увеличения каждого ребра в 3 раза, его объём будет равен 27 V.

, x=270 гр.

В кубе ABCDA₁B₁C₁D₁ найдите тангенс угла между прямой AС₁ и плоскостью BСC₁.

Из точки А опускаем перпендикуляр.

Т.к. , , то и

Тогда AC₁ – наклонная, ВС₁– проекция прямой AC₁ на плоскость BСC₁. Т.к. угол между прямой и плоскостью – это угол между этой прямой и её проекцией на плоскость, то — искомый.

Треугольник ABC₁— прямоугольный.

.

Пусть сторона куба равна a. Тогда .

.

Ответ: .

2.Сторона основания правильной призмы ABCDA₁B₁C₁D₁ равна 12, а боковое ребро.Найдите градусную меру угла между плоскостями AB₁C и ABC.

Плоскость AB₁C пересекает плоскость ABC по прямой AC. Построим линейный угол двугранного угла между этими плоскостями.

Для этого из точки B проведём перпендикуляр к прямой AC. Т.к. призма правильная, то её основанием является правильный четырёхугольник – квадрат. Диагонали квадрата взаимно перпендикулярны, следовательно, искомый перпендикуляр-отрезок BO – половина диагонали BD, причём точка O – середина отрезка AC.

Следовательно, угол BOB₁ является линейным углом двугранного угла между плоскостями AB₁C и ABC.

В квадрате ABCD AB=12, BD=, BO=:2 =

Рассмотрим треугольник BB₁O.

, следовательно, .

3. В прямоугольном параллелепипеде АВСДА₁В₁С₁Д₁найдите угол между плоскостью АА₁С и прямой А₁В, если АА₁=3, АВ=4, ВС= 4.

Решение. Из точки В проведем перпендикуляр ВН к АС. А₁Н – проекция А₁В на плоскость АА₁С. Значит, угол ВА₁Н- искомый.

Из прямоугольного треугольника АВС находим ВН=2.

Из прямоугольного треугольника А₁АВ находим А₁В= 5.

Из прямоугольного треугольника А₁НВ находим sinА₁==

Ответ: arcsin.

Задачи для самостоятельного решения.

1. Объём прямоугольного параллелепипеда равен 32. Чему будет равен объём

параллелепипеда, если каждое его ребро уменьшить в 2 раза. (4)

2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 36 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд той же формы, у которого сторона основания в 3 раза больше, чем у первого. Ответ выразите в сантиметрах. (4)

3. Закрытый сосуд в виде прямоугольного параллелепипеда с ребрами 30, 40 и 45 см. стоит на горизонтальной поверхности таким образом, что наименьшая грань является дном. В сосуд налили воду до уровня 36 см. На каком уровне окажется вода, если сосуд поставить на наибольшую грань? Ответ дайте в сантиметрах. ( 24 )

4. В кубе ABCDA₁B₁C₁D₁ найдите тангенс угла между прямой AA₁ и плоскостью BC₁D. ()

5. Основание прямой призмы АВСА₁В₁С₁— треугольник АВС, в котором, ВС=2, sinА=0,3. Высота призмы равна. Найдите синус угла между прямой ВС₁ и плоскостью АСС₁. ( 0,2)

6. В основании прямой призмы лежит равнобедренный треугольник с основанием, равным 6 см., и углом при вершине 120º. Диагональ боковой грани, содержащей основание равнобедренного треугольника, равна 10 см. Найдите площадь боковой поверхности. (48 +32)

Источник