объем конуса можно вычислить по формуле
Объем конуса
Объём конуса выражается такой же формулой, что и объём пирамиды: V = 1 /3 Sh,
где V — объём конуса, S — площадь основания конуса, h — его высота.
Окончательно V = 1 /3 πR 2 h, где R — радиус основания конуса.
Получение формулы объёма конуса можно пояснить таким рассуждением:
Пусть дан конус (рис). Впишем в него правильную пирамиду, т. е. построим внутри конуса такую пирамиду, вершина которой совпадает с вершиной конуса, а основанием служит правильный многоугольник, вписанный в основание конуса.
Объём этой пирамиды выразится формулой: V’ = 1 /3 S’h, где V — объём пирамиды,
S’ — площадь её основания, h — высота пирамиды.
Если при этом за основание пирамиды взять многоугольник с очень большим числом сторон, то площадь основания пирамиды будет весьма мало отличаться от площади круга, а объём пирамиды — весьма мало отличаться от объёма конуса. Если, пренебречь этими различиями в размерах, то объём конуса выразится следующей формулой:
V = 1 /3 Sh, где V — объём конуса, S — площадь основания конуса, h — высота конуса.
Примечание. В формуле V = 1 /3 Sh поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы его считать приближённым, но в старших классах средней школы доказывается, что равенство
V = 1 /3 Sh точное, а не приближённое.
Объем произвольного конуса
Теорема. Объем произвольного конуса равен одной трети произведения площади основания на высоту, т.е.
где Q — площадь основания, а Н — высота конуса.
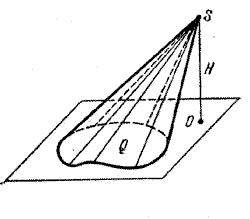
Рассмотрим конус с вершиной S и основанием Ф (рис.).
Пусть площадь основания Ф равна Q, а высота конуса равна Н. Тогда существуют последовательности многоугольников Фn и Ф’n с площадями Qn и Q’n таких, что
Очевидно, что пирамида с вершиной S и основанием Ф’n будет вписанной в данный конус, а пирамида с вершиной S и основанием Фn — описанной около конуса.
Объемы этих пирамид соответственно равны
то формула (1) доказана.
Следствие. Объем конуса, основанием которого является эллипс с полуосями а и b, вычисляется по формуле
В частности, объем конуса, основанием которого является круг радиуса R, вычисляется по формуле
где Н — высота конуса.
Как известно, площадь эллипса с полуосями а и b равна π ab, и поэтому формула (2) получается из (1) при Q = π ab. Если а = b = R, то получается формула (3).
Объем прямого кругового конуса
Теорема 1. Объем прямого кругового конуса с высотой Н и радиусом основания R вычисляется по формуле
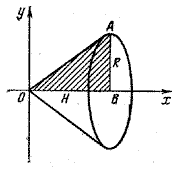
Данный конус можно рассматривать как тело, полученное вращением треугольника с вершинами в точках О(0; 0),В(Н; 0), А(Н; R) вокруг оси Ох (рис.).
Треугольник ОАВ является криволинейной трапецией, соответствующей функции
у = R /H х, х ∈ [0; H]. Поэтому, используя известную формулу, получаем
Следствие. Объем прямого кругового конуса равен одной трети произведения площади основания на высоту, т. е.
где Q — площадь основания, а H — высота конуса.
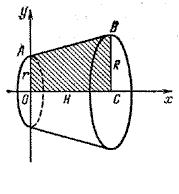
Теорема 2. Объем усеченного конуса с радиусами оснований r и R и высотой H вычисляется по формуле
Усеченный конус можно получить вращением вокруг оси Ох трапеции О ABC (рис.).
Прямая АВ проходит через точки (0; r) и (H; R), поэтому она имеет уравнение
Для вычисления интеграла сделаем замену
Очевидно, когда х изменяется в пределах от 0 до H, переменная и изменяется от r до R, и поэтому
Нахождение объема конуса: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать объем прямого кругового конуса и разберем примеры решения задач.
Формула вычисления объема
1. Через площадь основания и высоту
Объем (V) конуса равняется одной третьей произведения его высоты на площадь основания:
2. Через радиус основания и высоту
Следовательно, формулу для вычисления объема конуса можно представить в виде:
Т.е. объем конуса равняется одной третьей произведения его высоты на число π и на радиус основания в квадрате.
Примечание: в расчетах значение числа π округляется до 3,14.
Формула для нахождения объема усеченного конуса представлена в отдельной публикации.
Примеры задач
Решение:
Применим первую формулу, подставив в нее заданные значения:
Задание 2
Высота конуса равна 7 см, а его радиус – 3 см. Найдите объем фигуры.
Решение:
Воспользовавшись второй, более расширенной, формулой получаем:
Формула объема конуса
Круглый конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называют также конусом вращения.
Связанные определения для конуса
Образующая конуса. Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
Образующая поверхность конуса. Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.
Коническая поверхность. Образующая поверхность конуса является конической поверхностью.
Высота конуса (H). Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
Прямой конус. Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
Прямой круговой конус. Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
Эллиптическим конус. Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
Усечённый конус. Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
Объем прямого углового конуса
Первый способ вычисления объема конуса
Объем конуса равен одной трети произведения площади основания на высоту
Второй способ вычисления объема конуса
Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
\[ \LARGE V = \frac
Калькулятор объема конуса
Объем усеченного конуса
Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом.
Первый способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
\[ \LARGE V = \frac<1> <3>\left( H\cdot S_2 + h \cdot s_1 \right) \]
Второй способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
\[ \LARGE V = \frac<1> <3>\pi h \left( R^2 + R \cdot r + r^2 \right) \]
Объём конуса
Онлайн калькулятор
Через площадь основания и высоту

Высота h =
Через радиус и другие параметры

=
Теория
Объём конуса через площадь основания и высоту
Чему равен объём конуса V, если площадь его основания Sосн, а высота h:
Формула
Пример
Для примера посчитаем, чему равен объём конуса, у которого площадь основания Sосн = 3 см², а высота h = 5 см :
Объём конуса через образующую и радиус
Чему равен объём конуса V, если его образующая l, радиус основания r?
Формула
Пример
Для примера посчитаем, чему равен объём конуса, у которого образующая l = 5 см, а радиус основания r = 2 см:
Объём конуса через радиус и высоту
Чему равен объём конуса V, если радиус его основания r, а высота h?
Формула
Пример
Для примера посчитаем объём конуса, у которого высота h = 6 см, а радиус основания r = 3 см:
V = ⅓ ⋅ 3.14 ⋅ 3² ⋅ 6 = 169.56 /3 = 56.52 см³
Объём конуса через угол раствора (α) и радиус
Чему равен объём конуса V, если угол раствора α, а радиус основания r?
Формула
Пример
Для примера посчитаем объём конуса, имеющего угол раствора α = 30° и радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2³ /tg(30/2) ≈ 1,0467 ⋅ 8 / 0.2679 ≈ 31.25 см³
Объём конуса через угол β и радиус
Чему равен объём конуса V, если известны угол β и радиус основания r?
Формула
Пример
Для примера посчитаем объём конуса, имеющего угол β = 20° и радиус основания r = 3 см:
V = ⅓ ⋅ 3.14 ⋅ 3³ /tg 20 ≈ 1,0467 ⋅ 27 / 0.36397 ≈ 77.64 см³
Объём конуса через угол γ и радиус
Чему равен объём конуса V, если известны угол γ и радиус основания r?
Формула
Пример
Для примера посчитаем объём конуса, имеющего угол γ = 45° и радиус основания r = 2 см:
V = ⅓ ⋅ 3.14 ⋅ 2³ ⋅ tg 45 ≈ 1,0467 ⋅ 8 ⋅ 1 ≈ 8.37 см³
Объем конуса можно вычислить по формуле
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса.
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите
Объем конуса равен
где —площадь основания, а
— высота конуса. Высоту конуса найдем по свойству стороны прямоугольного треугольника, находящейся напротив угла в
°: — он вдвое меньше гипотенузы, которой в данном случае является образующая конуса. Радиус основания найдем по теореме Пифагора:
Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
Объем конуса равен
где — площадь основания, а
— высота конуса. При уменьшении высоты в 3 раза объем конуса также уменьшится в 3 раза.
V=1/3Sh-это формула объёма пирамиды!
Она же формула объема конуса.
В добавление замечу, что возможен ещё третий случай, когда высота конуса уменьшается в 3 раза (вообще говоря, в n раз): если образующая не меняется. При этом изменяются телесный угол (увеличивается), а радиус основания (увеличивается), так как образующая, высота и радиус основания конуса соответствующим образом связаны теоремой Пифагора. В данном случае ответ будет соответствующим образом зависеть от соотношения между образующей и радиусом основании исходного конуса. Например, если у исходного конуса положить угол между образующей и плоскость основания равным 45 град., то, в результате несложных вычислений, мы получим объём конуса (с уменьшенной в 3 раза высотой и той же самой образующей): V2 = 17/27*V1 или V2/V1 = 17/27.