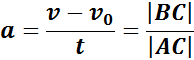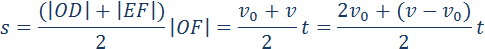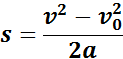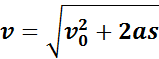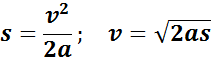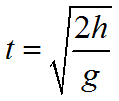по какой формуле можно определить скорость при равноускоренном прямолинейном движении
Равноускоренное движение
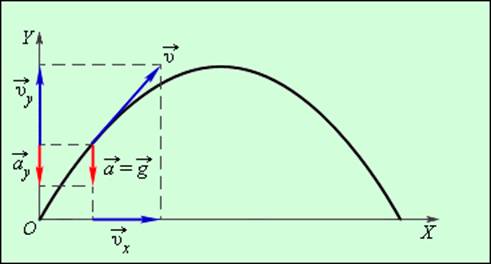
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения 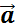
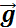
Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости 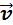
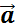
Проекции векторов скорости 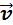
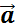
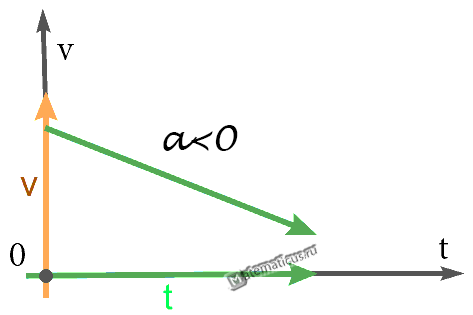
При равноускоренном прямолинейном движении скорость тела определяется формулой
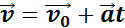
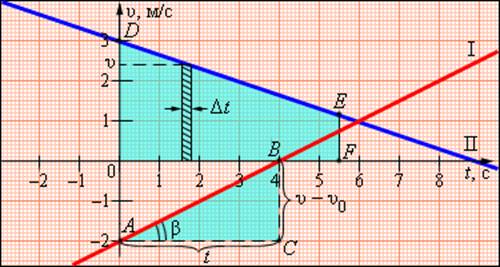
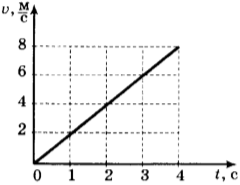
В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.4.2).
Графики скорости равноускоренного движения
По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC:
Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.
Для графика II: υ0 = 3 м/с, a = –1/3 м/с 2
График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.
Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:
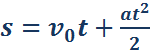
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:
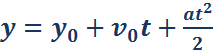
Это выражение называют законом равноускоренного движения.
При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде
Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и перемещение s:
Если начальная скорость υ0 равна нулю, эти формулы принимают вид
Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ0, υ, s, a, y0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.
Скорость при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Описывая движение с постоянной скоростью, мы могли с уверенностью сказать, какую скорость имеет тело в любой момент времени. В случае с равноускоренным движением это не так, потому что скорость постоянно меняется. Поэтому для его описания вводится понятие мгновенной скорости.
Скорость тела в момент времени t равна сумме начальной скорости тела в момент времени t0 и произведения ускорения этого тела на время t, в течение которого это тело двигалось. В векторном виде это записывается так:
v — скорость тела в данный момент времени, v 0 —скорость тела в начальный момент времени, a — ускорение тела, t — время, в течение которого это тело двигалось
Направление вектора скорости при равномерном равноускоренном движении не всегда совпадает с направлением вектора ускорения и вектором перемещения тела.
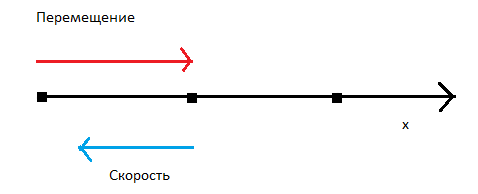
Пример №1. Мальчик пробежал 200 метров по прямой линии, а затем вернулся в исходное положение. Определить направление вектора скорости и перемещения в момент, когда мальчик, возвращаясь в исходное положение, находился на полпути до него.
Началу вектора перемещения соответствует исходное положение мальчика. Когда мальчик возвращался и находился на полпути до исходного положения, концу вектора его перемещения соответствовала точка, лежащая посередине 200-метрового отрезка. Поэтому вектор перемещения направлен в сторону ОХ. Но мальчик в это время направлялся в обратную сторону. Поэтому его скорость была направлена против направления оси ОХ.
Скалярная формула скорости
В случае равноускоренного прямолинейного движения можно вместо векторов использовать скаляры. Тогда формула примет следующий вид:
Знак «+» ставится в случае, когда тело разгоняется, знак «–» — когда оно тормозит.
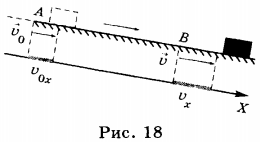
Проекция скорости
Проекция скорости при равноускоренном прямолинейном движении имеет вид:
Знак проекции скорости зависит от того, в какую сторону движется тело:
Знак проекции скорости не зависит от того, каким является движение: равнозамедленным или равноускоренным.
График скорости
График скорости — график зависимости проекции скорости от времени. Графиком скорости при равноускоренном прямолинейном движении является прямая.
Сравнение модулей ускорения по графикам скоростей
Чтобы сравнить модули ускорений по графикам скоростей, нужно сравнить их углы наклона к оси времени. Чем больше между ними угол, тем больше модуль ускорения. Так, на рисунке выше большим модулем ускорения обладает тело 3 — угол между его графиком скорости и осью времени максимальный. Меньшим модулем ускорения обладает тело 1, так как угол между его графиком скорости и осью времени минимальный.
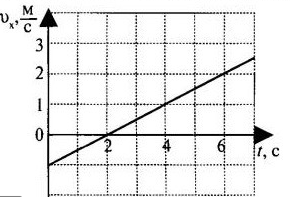
Пример №2. Ниже представлен график движения велосипедиста. Опишем характер его движения на участке от 0 до 2 с, в момент времени t=2 с и на участке от 2 с.
На отрезке пути от 0 до 2 с велосипедист двигался в направлении, противоположном оси ОХ. При этом модуль его скорости уменьшался. В момент времени t=2 c велосипедист приостановился и поменял направление движения, и дальше оно стало совпадать с осью ОХ. Модуль его скорости при этом начал расти. Но на всем пути независимо от направления движения велосипедиста вектор его ускорения всегда был направлен в сторону ОХ. Однако до 2 с движение считалось равнозамедленным, так как ускорение и скорость были направлены в противоположные стороны. После 2 с движение стало равноускоренным, так как направления скорости и ускорения совпали.
Пример №3. Грузовик ехал с некоторой постоянной скоростью. Затем он затормозил и остановился в течение 5 секунд. Найти постоянную скорость, с которой двигался грузовик, если при торможении модуль его ускорения составил 2 м/с.
Так как движение равнозамедленное, в формуле будем использовать» знак «–». Он будет указывать на то, что скорость грузовика с течением времени уменьшалась:
Выразим начальную скорость:
Так как грузовик в итоге остановился, его конечная скорость равна 0. Подставляем известные данные в формулу и получаем:

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Формулы равномерного и равноускоренного движения
Равномерное движение
Формула скорости движения при равномерном движении: 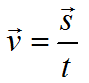
v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении: 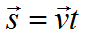
Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле: 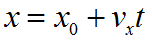
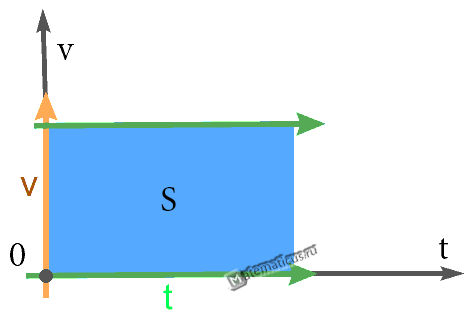
График — Равномерного прямолинейного движения
Равноускоренное движение
Формула скорости при равноускоренном движении: 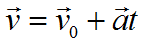
a=const
v0 — начальная скорость, м/с
a — ускорение, м/с 2
Формула для нахождения перемещения при равноускоренном движении: 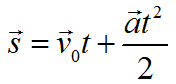
или 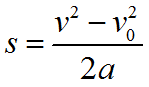
Уравнение равноускоренного движения в проекции на оси координат: 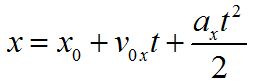
Формула для определения ускорения при равноускоренном прямолинейном движении: 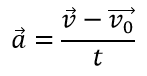
v0 — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения: 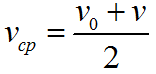
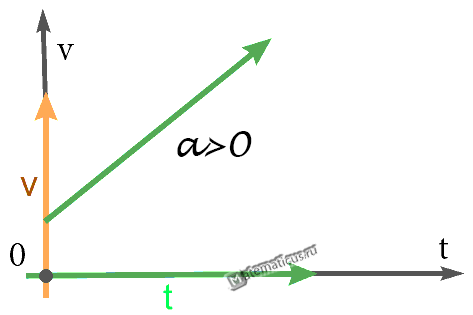
График — Равноускоренное движение при a>0
Равнозамедленное движение
Формула скорости при равнозамедленном движении: 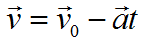
Формула перемещения при равнозамедленном движении: 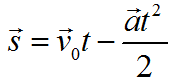
График — Равнозамедленное движение при a 2
Формула для вычисления скорости при свободном падении тела: 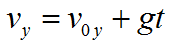
Формула для вычисления перемещения при свободном падении тела: 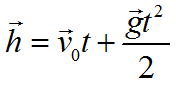
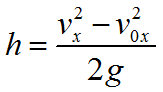
Формула координаты при свободном падении тела: 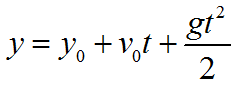
Формула высоты с которой тело свободно падает: 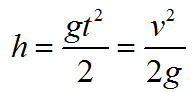
Формула для определения скорости тела в конце свободного падения: 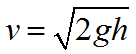
Время свободного падения тела равно:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.8 / 5. Количество оценок: 33
Скорость. Ускорение. Равноускоренное прямолинейное движение
1. Реальное механическое движение — это движение с изменяющейся скоростью. Движение, скорость которого стечением времени изменяется, называют неравномерным движением.
При неравномерном движении координату тола уже нельзя определить но формуле \( x=x_0+v_xt \) , так как значение скорости движения не является постоянным. Поэтому для характеристики быстроты изменения положения тела с течением времени при неравномерном движении вводят величину, называемую средней скоростью.
Средней скоростью \( \vec\) тела ко времени \( t \) , за которое оно произошло: \( \vec
2. Важно, что, зная среднюю скорость неравномерного движения на каком-либо участке траектории, нельзя определить положение тела на этой траектории в любой момент времени. Например, если средняя скорость движения автомобиля за 2 часа 50 км/ч, то мы не можем сказать, где он находился через 0,5 часа от начала движения, через 1 час, 1,5 часа и т.п., поскольку он мог первые полчаса двигаться со скоростью 80 км/ч, затем какое-то время стоять, а какое-то время ехать в пробке со скоростью 20 км/ч.
3. Двигаясь по траектории, тело проходит последовательно все её точки. В каждой точке траектории оно находится в определённые моменты времени и имеет какую-то скорость.
Мгновенной скоростью называют скорость тела в данный момент времени в данной точке траектории.
При дальнейшем уменьшении перемещения и соответственно времени движения тела они станут такими маленькими, что прибор, например спидометр, перестанет фиксировать изменение скорости, и движение за этот малый промежуток времени можно считать равномерным. Средняя скорость на этом участке и есть мгновенная скорость тела в т.О.
4. Одним из видов неравномерного движения является равноускоренное движение. Равноускоренным движением называют движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение.
Слова «любые равные промежутки времени» означают, что какие бы равные промежутки времени (2 с, 1 с, доли секунды и т.п.) мы ни взяли, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.
5. Характеристикой равноускоренного движения, помимо скорости и перемещения, является ускорение.
Ускорение тела при равноускоренном движении — векторная физическая величина, равная отношению изменения скорости тела к промежутку времени, за который это изменение произошло.
Направление ускорения совпадает с направлением скорости движения, если модуль скорости увеличивается, ускорение направлено противоположно скорости движения, если модуль скорости уменьшается.
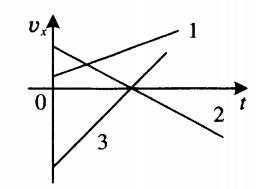
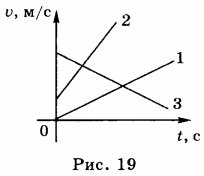
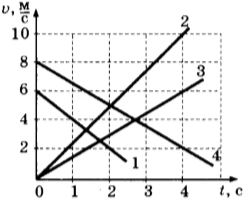
7. Как видно из формулы скорости равноускоренного движения, она линейно зависит от времени. Графиком зависимости модуля скорости от времени является прямая, составляющая некоторый угол с осью абсцисс (осью времени). На рисунке 19 приведены графики зависимости модуля скорости от времени.
График 1 соответствует движению без начальной скорости с ускорением, направленным так же, как и скорость; график 2 — движению с начальной скоростью \( v_ <02>\) и с ускорением, направленным так же, как и скорость; график 3 — движению с начальной скоростью \( v_ <03>\) и с ускорением, направленным в сторону, противоположную направлению скорости.
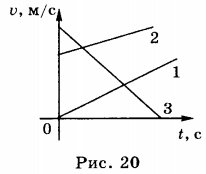
8. На рисунке приведены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).
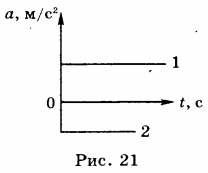
9. На рисунке 21 приведены графики зависимости проекции ускорения равноускоренного движения от времени.
График 1 соответствует движению, проекция ускорения которого положительна, график 2 — движению, проекция ускорения которого отрицательна.
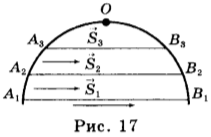
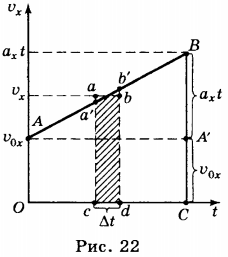
10. Формулу перемещения тела при равноускоренном движении можно получить, используя график зависимости проекции скорости этого движения от времени (рис. 22).
Выделим на графике малый участок \( ab \) и опустим перпендикуляры из точек \( a \) и \( b \) на ось абсцисс. Если промежуток времени \( \Delta
На такие полоски можно разбить всю фигуру ОАВС, и её площадь равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время \( t \) численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: \( S_x= \frac<1><2>(OA+BC)OC \) .
Полученная формула позволяет определить положение (координату) тела в любой момент времени, если известны начальная скорость, начальная координата и ускорение.
Если начальная скорость тела равна нулю, то: \( v^2_x=2a_xs_x \) .
Полученная формула позволяет рассчитать тормозной путь транспортных средств, т.е. путь, который проезжает, например, автомобиль до полной остановки. При некотором ускорении движения, которое зависит от массы автомобиля и силы тяги двигателя, тормозной путь тем больше, чем больше начальная скорость автомобиля.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
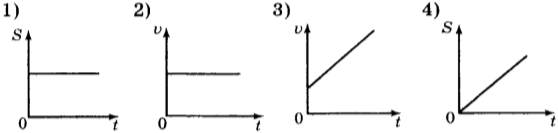
1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?
2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?
1) 200 м/с 2
2) 20 м/с 2
3) 2 м/с 2
4) 0,5 м/с 2
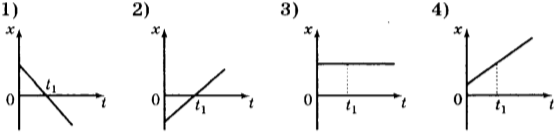
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси \( Оx \) . У какого из тел в момент времени \( t_1 \) скорость движения равна нулю?
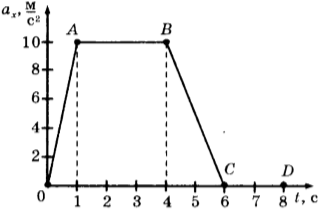
4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси \( Оx \) .
Равноускоренному движению соответствует участок
1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD
5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.
Чему равен путь, пройденный телом за третью секунду?
1) 4 м
2) 4,5 м
3) 5 м
4) 9 м
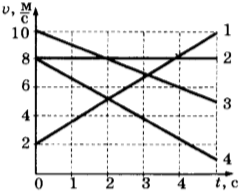
6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.
Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?
1) только 1
2) только 2
3) только 4
4) 3 и 4
7. Используя график зависимости скорости движения тела от времени, определите его ускорение.
8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?
1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с
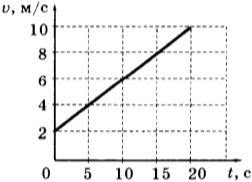
10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.
1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с
11. Два тела движутся по оси \( Оx \) . На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) В промежутке времени \( t_3-t_5 \) тело 2 движется равноускоренно.
2) К моменту времени \( t_2 \) от начала движения тела прошли одинаковые пути.
3) В промежутке времени \( 0-t_3 \) тело 2 находится в покое.
4) В момент времени \( t_5 \) тело 1 останавливается.
5) В промежутке времени \( t_3-t_4 \) ускорение \( a_x \) тела 1 отрицательно.
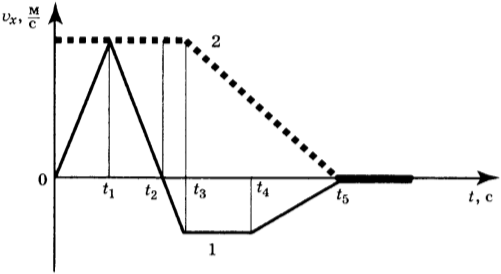
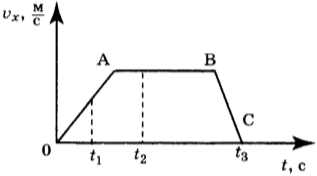
12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени \( t_1 \) тело имело максимальное по модулю ускорение.
4) Момент времени \( t_3 \) соответствует остановке тела.
5) В момент времени \( t_2 \) тело имело максимальное по модулю ускорение.
Часть 2
13. Зависимость координаты от времени для некоторого тела описывается уравнением \( x=12t-t^2 \) . В какой момент времени скорость движения равна нулю?