скнф логической функции можно определить как

23.03.202331.03.2023 admin 0 Comments

Скнф логической функции можно определить как

Определение:

Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.

Пример КНФ: [math]f(x,y,z) = (x \lor y) \land (y \lor \neg)[/math]

СКНФ [ править ]

Пример СКНФ: [math]f(x,y,z) = (x \lor \neg \lor z) \land (x\lor y \lor \neg)[/math]

Последнее выражение и является СКНФ. Так как СКНФ получена из СДНФ, которая может быть посторена для любой функции, не равной тождественному нулю, то теорема доказана.[math]\triangleleft[/math]

Алгоритм построения СКНФ по таблице истинности [ править ]

Пример построения СКНФ для медианы [ править ]

Построение СКНФ для медианы от трех аргументов [ править ]

0	0	0	0
x	y	z	[math] \langle x,y,z \rangle [/math]
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

0	0	0	0	[math]( x \lor y \lor z)[/math]
x	y	z	[math] \langle x,y,z \rangle [/math]
0	0	1	0	[math]( x \lor y \lor \neg)[/math]
0	1	0	0	[math](x \lor \neg \lor z)[/math]
0	1	1	1
1	0	0	0	[math](\neg \lor y \lor z)[/math]
1	0	1	1
1	1	0	1
1	1	1	1

3. Все полученные дизъюнкции связываем операциями конъюнкции.

[math] \langle x,y,z \rangle = ( x \lor y \lor z) \land (\neg \lor y \lor z) \land (x \lor \neg \lor z) \land ( x \lor y \lor \neg)[/math]

Построение СКНФ для медианы от пяти аргументов [ править ]

0	0	0	0	0	0	[math](x_1 \lor x_2 \lor x_3 \lor x_4 \lor x_5)[/math]
[math] x_1 [/math]	[math] x_2 [/math]	[math] x_3 [/math]	[math]x_4[/math]	[math] x_5 [/math]	[math] \langle x_1, x_2, x_3, x_4, x_5 \rangle [/math]
0	0	0	0	1	0	[math](x_1 \lor x_2 \lor x_3 \lor x_4 \lor \neg )[/math]
0	0	0	1	0	0	[math](x_1 \lor x_2 \lor x_3 \lor \neg \lor x_5)[/math]
0	0	0	1	1	0	[math](x_1 \lor x_2 \lor x_3 \lor \neg \lor \neg )[/math]
0	0	1	0	0	0	[math](x_1 \lor x_2 \lor \neg \lor x_4 \lor x_5)[/math]
0	0	1	0	1	0	[math](x_1 \lor x_2 \lor \neg \lor x_4 \lor \neg )[/math]
0	0	1	1	0	0	[math](x_1 \lor x_2 \lor \neg \lor \neg \lor x_5)[/math]
0	0	1	1	1	1
0	1	0	0	0	0	[math](x_1 \lor \neg \lor x_3 \lor x_4 \lor x_5)[/math]
0	1	0	0	1	0	[math](x_1 \lor \neg \lor x_3 \lor x_4 \lor \neg )[/math]
0	1	0	1	0	0	[math](x_1 \lor \neg \lor x_3 \lor \neg \lor x_5)[/math]
0	1	0	1	1	1
0	1	1	0	0	0	[math](x_1 \lor \neg \lor \neg \lor x_4 \lor x_5)[/math]
0	1	1	0	1	1
0	1	1	1	0	1
0	1	1	1	1	1
1	0	0	0	0	0	[math](\neg \lor x_2 \lor x_3 \lor x_4 \lor x_5)[/math]
1	0	0	0	1	0	[math](\neg \lor x_2 \lor x_3 \lor x_4 \lor \neg )[/math]
1	0	0	1	0	0	[math](\neg \lor x_2 \lor x_3 \lor \neg \lor x_5)[/math]
1	0	0	1	1	1
1	0	1	0	0	0	[math](\neg \lor x_2 \lor \neg \lor x_4 \lor x_5)[/math]
1	0	1	0	1	1
1	0	1	1	0	1
1	0	1	1	1	1
1	1	0	0	0	0	[math](\neg \lor \neg \lor x_3 \lor x_4 \lor x_5)[/math]
1	1	0	0	1	1
1	1	0	1	0	1
1	1	0	1	1	1
1	1	1	0	0	1
1	1	1	0	1	1
1	1	1	1	0	1
1	1	1	1	1	1

[math] \langle x_1, x_2, x_3, x_4, x_5 \rangle = (x_1 \lor x_2 \lor x_3 \lor x_4 \lor x_5) \land (x_1 \lor x_2 \lor x_3 \lor x_4 \lor \overline ) \land \\ (x_1 \lor x_2 \lor x_3 \lor \overline \lor x_5) \land (x_1 \lor x_2 \lor x_3 \lor \overline \lor \overline ) \land (x_1 \lor x_2 \lor \overline \lor x_4 \lor x_5) \land \\ (x_1 \lor x_2 \lor \overline \lor x_4 \lor \overline ) \land (x_1 \lor x_2 \lor \overline \lor \overline \lor x_5) \land (x_1 \lor \overline \lor x_3 \lor x_4 \lor x_5) \land \\ (x_1 \lor \overline \lor x_3 \lor x_4 \lor \overline ) \land (x_1 \lor \overline \lor x_3 \lor \overline \lor x_5) \land (x_1 \lor \overline \lor \overline \lor x_4 \lor x_5) \land (\overline \lor x_2 \lor x_3 \lor x_4 \lor x_5) \land (\overline \lor x_2 \lor x_3 \lor x_4 \lor \overline ) \land (\overline \lor x_2 \lor x_3 \lor \overline \lor x_5) \land (\overline \lor x_2 \lor \overline \lor x_4 \lor x_5) \land (\overline \lor \overline \lor x_3 \lor x_4 \lor x_5) [/math]

Примеры СКНФ для некоторых функций [ править ]

Стрелка Пирса: [math] x \downarrow y = (\neg \lor ) \land ( \lor \neg ) \land (\neg \lor \neg ) [/math]

Исключающее или: [math] x \oplus y \oplus z = (\neg \lor \neg \lor z) \land (\neg \lor y \lor \neg ) \land (x \lor \neg \lor \neg ) \land (x \lor y \lor z)[/math]

Источник

Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения

Что такое СДНФ

Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.

Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).

СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».

ДНФ выглядит следующим образом:

СДНФ обладает некоторыми определенными свойствами:

К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.

При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.

Что такое СКНФ

СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.

Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:

Правила построения по таблице истинности

Дизъюнктивная форма

Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.

Конъюнктивная форма

Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.

Алгоритм приведения к СДНФ и СКНФ

Рассмотрим логическую функцию в виде таблицы истинности.

$скнф логической функции можно определить как. 54cafa 1 1602144234. скнф логической функции можно определить как фото. скнф логической функции можно определить как-54cafa 1 1602144234. картинка скнф логической функции можно определить как. картинка 54cafa 1 1602144234. Пример КНФ: f(x,y,z) = (x \lor y) \land (y \lor \neg)$

Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:

Построим совершенную ДНФ:

$скнф логической функции можно определить как. 9b35dd 2 1602144246. скнф логической функции можно определить как фото. скнф логической функции можно определить как-9b35dd 2 1602144246. картинка скнф логической функции можно определить как. картинка 9b35dd 2 1602144246. Пример КНФ: f(x,y,z) = (x \lor y) \land (y \lor \neg)$

И как результат получим следующую СДНФ:

Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:

Построим совершенную КНФ:

$скнф логической функции можно определить как. 43f339 3 1602144333. скнф логической функции можно определить как фото. скнф логической функции можно определить как-43f339 3 1602144333. картинка скнф логической функции можно определить как. картинка 43f339 3 1602144333. Пример КНФ: f(x,y,z) = (x \lor y) \land (y \lor \neg)$

И как результат получим следующую СКНФ:

Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.

Доказательство эквивалентности

Доказать эквивалентность формул можно двумя способами.

Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.

Поглощение

Склеивание

Обобщенное склеивание

$xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z$

$xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z$

Расщепление

$x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y$

Примеры с решением

Задача №1

Через применение закона де Моргана и правила $ x\;\rightarrow\;y\;=\;\overline x\;\vee\;y$ упростим выражения:

$F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=$

$=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline<((\overline A\;\vee\;B)>\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=$

$=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline<(\overline<(\overline A\vee B)>\;\vee\;\overline A\;)>\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=$

$=\;((\overline<(\overline A\;\vee\;B)>\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=$

$=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=$

$=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C$

Далее приведем выражение к КНФ:

$F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)$

Далее приведем выражение к СКНФ:

$F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=$

$=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)$

Задача №2

Используя эквивалентные преобразования, постройте ДНФ функции $f(\widetilde x^n)$

$f(\widetilde x^3) = (\overlinex_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2)$

$f(\widetilde x^3) = (\overlinex_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2) = ((\overlinex_2\;\cdot\;\overline\;)\;\vee\;(\overline<\overlinex_2>\;\cdot\;x_3))\;\cdot\;(\overline\;\vee\;x_2)\;=$

$=(\overlinex_2\overline\;\cdot(x_1\vee x_3\vee x_2)\;\vee\;x_1x_3\;\cdot\;(\overline\;\vee\;\overline\;\vee\;x_2)\;\vee\;\overlinex_3\;\cdot\;(\overline\;\vee\;\overline\;\vee\;x_2))\;=$

Источник

СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице

Простой дизъюнкцией < англ. inclusive disjunction >или дизъюнктом < англ. disjunct >называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.

Конъюнктивная нормальная форма, КНФ < англ. conjunctive normal form, CNF >нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.

Совершенная конъюнктивная нормальная форма, СКНФ < англ. perfect conjunctive normal form, PCNF >— это такая КНФ, которая удовлетворяет условиям:

Найдём инверсию левой и правой части выражения:

Последнее выражение и является СКНФ. Так как СКНФ получена из СДНФ, которая может быть построена для любой функции, не равной тождественному нулю, то теорема доказана.

Алгоритм построения СКНФ по таблице истинности

Пример построения СКНФ для медианы

3). Все полученные дизъюнкции связываем операциями конъюнкции.

$ \langle x,y,z \rangle = ( x \lor y \lor z) \land (\neg < x >\lor y \lor z) \land (x \lor \neg < y >\lor z) \land ( x \lor y \lor \neg < z >)$

Примеры СКНФ для некоторых функций

Полином Жегалкина. Пример.

Специальные векторные поля

Вычисление двойного интеграла

Примеры применения цилиндрических и сферических координат

Дифференциальные характеристики векторного поля

Критерий полноты <формулировка>. Лемма о нелинейной функции

Поверхностный интеграл первого рода и его свойства

Вычисление поверхностного интеграла второго рода

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Вычисление поверхностного интеграла первого рода

Свойства двойного интеграла

Критерий полноты

Вычисление площади поверхности

Источник

Опорный конспект на тему «Построение СКНФ и СДНФ»

$скнф логической функции можно определить как. 0e88 00098467 491b1f44. скнф логической функции можно определить как фото. скнф логической функции можно определить как-0e88 00098467 491b1f44. картинка скнф логической функции можно определить как. картинка 0e88 00098467 491b1f44. Пример КНФ: f(x,y,z) = (x \lor y) \land (y \lor \neg)$

Построение СДНФ и СКНФ.

Нормальные формы логических функций.

Одна и та же логическая функция может быть задана разными выражениями (формулами), иногда довольно сложными. Для сравнения выражений их следует упростить. Под упрощением выражений понимают равносильные преобразования, приводящие к нормальной форме.

Логическое выражение имеет нормальную форму, если в нем используются только три логические операции: дизъюнкции, конъюнкции и отрицания переменных. При этом не используется двойное отрицание и отрицание выражений.

Элементарная конъюнкция – логическое произведение аргументов или их отрицаний. Например, А ∧ ¬В ∧ С – элементарная конъюнкция, а ¬ (А ∧ ¬В) – нет, т.к. присутствует отрицание выражения.

Элементарная дизъюнкция – логическая сумма аргументов или их отрицаний, например, А ∨ ¬В ∨ С – элементарная дизъюнкция, а ¬ (А ∨ ¬В) – нет, т.к. присутствует отрицание выражения. Выражение А ∨ ¬В ∧ С также не является элементарной дизъюнкцией, т.к. в него входит конъюнкция.

Если каждый аргумент входит в элементарную конъюнкцию (дизъюнкцию) не более одного раза, она называется правильной элементарной конъюнкцией (дизъюнкцией).

Ранг элементарной конъюнкции или дизъюнкции – число аргументов ее образующих.

Дизъюнктивная нормальная форма (ДНФ) – это дизъюнкция попарно различных правильных элементарных конъюнкций (логическая сумма логических произведений), например, (X ∧ Y) ∨ (¬X ∧ Y ∧ Z) ∨ (X ∧ ¬Y ∧ Z).

Конъюнктивная нормальная форма (КНФ) – это конъюнкция попарно различных правильных элементарных дизъюнкций (логическое произведение логических сумм), например, (X ∨ Y) ∧ (¬X ∨ Y ∨ Z) ∧ (X ∨ ¬Y ∨ Z).

Любая логическая функция приводится к ДНФ или КНФ с помощью следующего алгоритма:

1) избавляются от импликации, эквивалентности, исключающего ИЛИ;

2) избавляются от отрицаний над сложными высказываниями, используя закон де Моргана и закон двойного отрицания;

3) раскрывают скобки, применяя дистрибутивные (распределительные) законы логики.

4) уменьшают количество вхождений переменных, используя законы алгебры логики.

Укажите, какое логическое выражение равносильно выражению ¬( А ∧ ¬B ∧ ¬C)

1) ¬A ∨ B ∨ C 2) ¬A ∨ B ∨ ¬C 3) ¬A ∧ B ∧ C 4) A ∧ B ∧ ¬C

Решение: все предложенные варианты ответов представляют собой нормальные формы логических выражений. Приведем исходное выражение к нормальной форме, используя закон де Моргана, получим ¬А ∨ B ∨ C.

Решение: все предложенные варианты ответов представлены в нормальной форме. Приведем исходное выражение к нормальной форме, используя законы де Моргана, двойного отрицания и поглощения.

Запишем эти же преобразования, используя другие обозначения логических операций:

При решении заданий можно использовать любую форму записи. Определите, какая форма более наглядна и удобна для Вас.

Элементарная конъюнкция (дизъюнкция) называется полной относительно аргументов функции, если каждая переменная входит в нее ровно один раз (либо с отрицанием, либо без него).

Совершенной дизъюнктивной нормальной формой (СДНФ) функции называется дизъюнкция полных правильных элементарных конъюнкций, равных единице на тех же наборах, что и функция.

Совершенной конъюнктивной нормальной формой (СКНФ) функции называется конъюнкция полных правильных элементарных дизъюнкций, равных нулю на тех же наборах, что и функция.

Алгоритм образования СКНФ по таблице истинности.

1. Выделить в таблице истинности все строки, в которых функция принимает значения 0.

2. Для каждого выбранного набора записать элементарные дизъюнкции, содержащие переменные: а) если значение переменной равно 0, то записывается сама переменная, б) если значение переменной равно 1, то записывается инверсия этой переменной.

3. Соединить элементарные дизъюнкции знаком конъюнкции.

Алгоритм образования СДНФ по таблице истинности.

1. Выделить в таблице истинности все строки, в которых функция принимает значения 1.

2. Для каждого выбранного набора записать элементарные конъюнкции, содержащие переменные: а) если значение переменной равно 0, то записывается инверсия этой переменной, б) если значение переменной равно 1, то записывается сама переменная.

3. Соединить элементарные конъюнкции знаком дизъюнкции.

Построение СДНФ по таблице истинности.

Любую функцию, кроме констант 0 и 1, можно представить в виде как СДНФ, так и СКНФ.

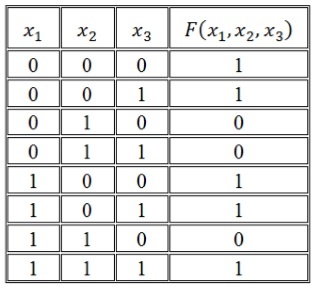
Рассмотрим решение задач на примере. Пусть две логические функции трех переменных заданы таблицей истинности.

Для функции F ₁ (A,B,C) построим СДНФ. По определению количество полных конъюнкций (слагаемых, представляющих собой произведение всех аргументов функции с отрицанием или без) равно количеству единиц в таблице истинности. В данном примере три единицы – на наборах 3, 5, 7.

1) Для каждой строки таблицы истинности, содержащей единицу, строим полную конъюнкцию (произведение аргументов). Переменные, имеющие нуль в соответствующей строке, входят в произведение с отрицанием. Переменные, имеющие значение единицы – без отрицания.

2) Запишем дизъюнкцию конъюнкций (сумму произведений)

Получена СДНФ. Если потребуется минимизировать количество вхождений аргументов, можно упростить выражение, используя законы алгебры логики.

Построим СКНФ функции F2(A,B,C) по таблице истинности

1) Для каждой строки таблицы истинности с нулевым значением функции (наборы 2, 6, 7) запишем полную дизъюнкцию (логическую сумму аргументов), переменные, имеющие значения 1 в строке, входят в эту сумму с отрицанием, а переменные со значением 0 – без отрицания:

2) Все полученные дизъюнкции (логические суммы) связываются операциями конъюнкции.

F ₂ (A,B,C) = (А ∨ ¬В ∨ С) ∧ (¬А ∨ ¬В ∨ С) ∧ (¬А ∨ ¬В ∨ ¬С).

Выбор способа построения логической функции зависит от количества 0 и 1 в таблице истинности функции: если в ней меньше 1, то лучше строить СДНФ и наоборот.

Анализ, упрощение и синтез логических схем.

Анализ логических схем.

Определение всех возможных условий протекания электрического тока. Это сводится к определению логической функции, соответствующей этой схеме и составлению таблицы истинности.

По полученной формуле строится таблица истинности, проводится анализ данной схемы:

Определяются исходные данные X и Y, при которых значение логической функции равно 1.

Упрощение логической схемы.

Упрощение логической схемы сводится к упрощению соответствующей ей формулы с использованием законов логики.

Синтез логической схемы.

Синтез логической схемы заключается в разработке схемы, условие работы которой задано таблицей истинности или словесным описанием.

Для синтеза логической схемы используется СДНФ или СКНФ.